In mathematics and computer science, currying is the technique of translating the evaluation of a function that takes multiple arguments into evaluating a sequence of functions, each with a single argument. For example, currying a function that takes three arguments creates a nested unary function , so that the code
In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions. It is a declarative programming paradigm in which function definitions are trees of expressions that map values to other values, rather than a sequence of imperative statements which update the running state of the program.
Lambda calculus is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation that can be used to simulate any Turing machine. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics.
In mathematics, logic, and computer science, a type theory is the formal presentation of a specific type system, and in general, type theory is the academic study of type systems. Some type theories serve as alternatives to set theory as a foundation of mathematics. Two influential type theories that were proposed as foundations are Alonzo Church's typed λ-calculus and Per Martin-Löf's intuitionistic type theory. Most computerized proof-writing systems use a type theory for their foundation, a common one is Thierry Coquand's Calculus of Inductive Constructions.
In mathematics and computer science in general, a fixed point of a function is a value that is mapped to itself by the function.
Curry's paradox is a paradox in which an arbitrary claim F is proved from the mere existence of a sentence C that says of itself "If C, then F", requiring only a few apparently innocuous logical deduction rules. Since F is arbitrary, any logic having these rules allows one to prove everything. The paradox may be expressed in natural language and in various logics, including certain forms of set theory, lambda calculus, and combinatory logic.
In programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and mathematical proofs.
In programming language theory and type theory, polymorphism is the provision of a single interface to entities of different types or the use of a single symbol to represent multiple different types. The concept is borrowed from a principle in biology where an organism or species can have many different forms or stages.
In computer programming, especially functional programming and type theory, an algebraic data type (ADT) is a kind of composite type, i.e., a type formed by combining other types.
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered. From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus, but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.
System F is a typed lambda calculus that introduces, to simply typed lambda calculus, a mechanism of universal quantification over types. System F formalizes parametric polymorphism in programming languages, thus forming a theoretical basis for languages such as Haskell and ML. It was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds.
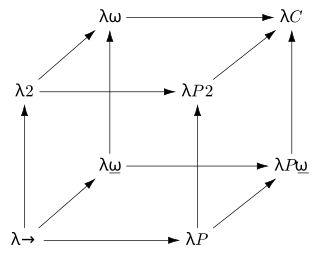
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
In computer science and logic, a dependent type is a type whose definition depends on a value. It is an overlapping feature of type theory and type systems. In intuitionistic type theory, dependent types are used to encode logic's quantifiers like "for all" and "there exists". In functional programming languages like Agda, ATS, Coq, F*, Epigram, and Idris, dependent types help reduce bugs by enabling the programmer to assign types that further restrain the set of possible implementations.
The simply typed lambda calculus, a form of type theory, is a typed interpretation of the lambda calculus with only one type constructor that builds function types. It is the canonical and simplest example of a typed lambda calculus. The simply typed lambda calculus was originally introduced by Alonzo Church in 1940 as an attempt to avoid paradoxical use of the untyped lambda calculus.
In mathematics and computer science, apply is a function that applies a function to arguments. It is central to programming languages derived from lambda calculus, such as LISP and Scheme, and also in functional languages. It has a role in the study of the denotational semantics of computer programs, because it is a continuous function on complete partial orders. Apply is also a continuous function in homotopy theory, and, indeed underpins the entire theory: it allows a homotopy deformation to be viewed as a continuous path in the space of functions. Likewise, valid mutations (refactorings) of computer programs can be seen as those that are "continuous" in the Scott topology.
In computer science, Scott encoding is a way to represent (recursive) data types in the lambda calculus. Church encoding performs a similar function. The data and operators form a mathematical structure which is embedded in the lambda calculus.
In the area of mathematical logic and computer science known as type theory, a kind is the type of a type constructor or, less commonly, the type of a higher-order type operator. A kind system is essentially a simply typed lambda calculus "one level up", endowed with a primitive type, denoted and called "type", which is the kind of any data type which does not need any type parameters.
In computer science, polymorphic recursion refers to a recursive parametrically polymorphic function where the type parameter changes with each recursive invocation made, instead of staying constant. Type inference for polymorphic recursion is equivalent to semi-unification and therefore undecidable and requires the use of a semi-algorithm or programmer-supplied type annotations.
A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.
In mathematical logic, System U and System U− are pure type systems, i.e. special forms of a typed lambda calculus with an arbitrary number of sorts, axioms and rules. They were both proved inconsistent by Jean-Yves Girard in 1972. This result led to the realization that Martin-Löf's original 1971 type theory was inconsistent as it allowed the same "Type in Type" behaviour that Girard's paradox exploits.

