In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.
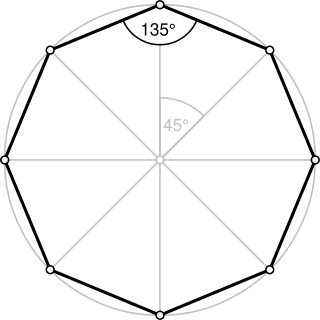
In geometry, an octagon is an eight-sided polygon or 8-gon.

In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.

In geometry, a nonagon or enneagon is a nine-sided polygon or 9-gon.

In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.

In geometry, a dodecagon or 12-gon is any twelve-sided polygon.

In geometry, a chiliagon or 1000-gon is a polygon with 1,000 sides. Philosophers commonly refer to chiliagons to illustrate ideas about the nature and workings of thought, meaning, and mental representation.

In geometry, a myriagon or 10000-gon is a polygon with 10,000 sides. Several philosophers have used the regular myriagon to illustrate issues regarding thought.
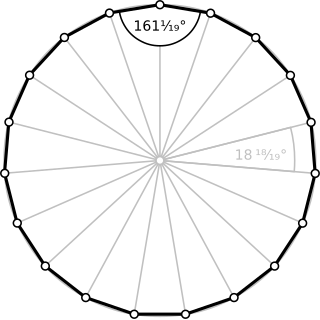
In geometry, an enneadecagon, enneakaidecagon, nonadecagon or 19-gon is a polygon with nineteen sides.

In geometry, a hendecagon or 11-gon is an eleven-sided polygon.

In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.

In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
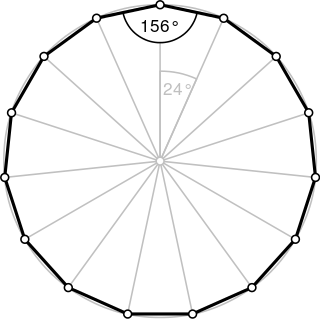
In geometry, a pentadecagon or pentakaidecagon or 15-gon is a fifteen-sided polygon.

In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non-self-intersecting 257-gon is 45,900°.

In geometry, a 65537-gon is a polygon with 65,537 (216 + 1) sides. The sum of the interior angles of any non-self-intersecting 65537-gon is 11796300°.

In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.

In mathematics, a hexadecagon is a sixteen-sided polygon.

A megagon or 1 000 000-gon is a polygon with one million sides.

In geometry, an icositetragon or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees.

In geometry, a tetracontadigon or 42-gon is a forty-two-sided polygon. The sum of any tetracontadigon's interior angles is 7200 degrees.