
The Mercator projection is a cylindrical map projection presented by Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for navigation because it is unique in representing north as up and south as down everywhere while preserving local directions and shapes. The map is thereby conformal. As a side effect, the Mercator projection inflates the size of objects away from the equator. This inflation is very small near the equator but accelerates with increasing latitude to become infinite at the poles. As a result, landmasses such as Greenland, Antarctica, Canada and Russia appear far larger than they actually are relative to landmasses near the equator, such as Central Africa.
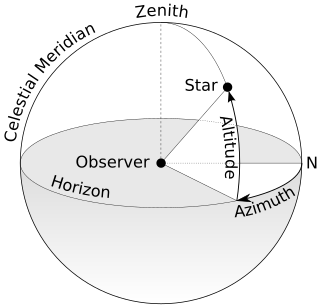
An azimuth is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north.

In navigation, a rhumb line, rhumb, or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north.

Orthographic projection in cartography has been used since antiquity. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic projection is at infinite distance. It depicts a hemisphere of the globe as it appears from outer space, where the horizon is a great circle. The shapes and areas are distorted, particularly near the edges.

The Craig retroazimuthal map projection was created by James Ireland Craig in 1909. It is a modified cylindrical projection. As a retroazimuthal projection, it preserves directions from everywhere to one location of interest that is configured during construction of the projection. The projection is sometimes known as the Mecca projection because Craig, who had worked in Egypt as a cartographer, created it to help Muslims find their qibla. In such maps, Mecca is the configurable location of interest.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians as straight, with distances from the pole represented correctly. The flag of the United Nations contains an example of a polar azimuthal equidistant projection.

The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, the concept of scale becomes meaningful in two distinct ways.
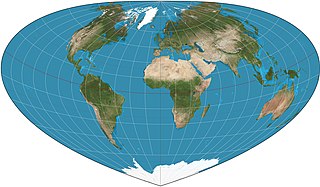
The Bottomley map projection is a pseudoconical equal area map projection defined as:
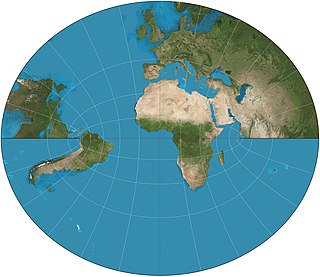
The Littrow projection is a map projection developed by Joseph Johann von Littrow in 1833. It is the only conformal, retroazimuthal map projection. As a retroazimuthal projection, the Littrow shows directions, or azimuths, correctly from any point to the center of the map.

In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.

The Winkel tripel projection, a modified azimuthal map projection of the world, is one of three projections proposed by German cartographer Oswald Winkel in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection: The name tripel refers to Winkel's goal of minimizing three kinds of distortion: area, direction, and distance.

The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide.

The Cassini projection is a map projection described by César-François Cassini de Thury in 1745. It is the transverse aspect of the equirectangular projection, in that the globe is first rotated so the central meridian becomes the "equator", and then the normal equirectangular projection is applied. Considering the earth as a sphere, the projection is composed of the operations:
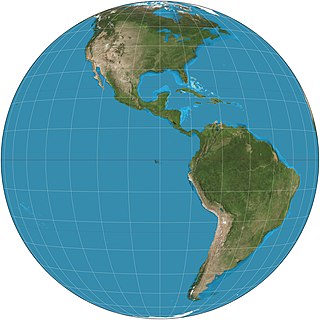
The General Perspective projection is a map projection. When the Earth is photographed from space, the camera records the view as a perspective projection. When the camera is aimed toward the center of the Earth, the resulting projection is called Vertical Perspective. When aimed in other directions, the resulting projection is called a Tilted Perspective.

The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west.

The Hammer retroazimuthal projection is a modified azimuthal proposed by Ernst Hermann Heinrich Hammer in 1910. As a retroazimuthal projection, azimuths (directions) are correct from any point to the designated center point. Additionally, all distances from the center of the map are proportional to what they are on the globe. In whole-world presentation, the back and front hemispheres overlap, making the projection a non-injective function. The back hemisphere can be rotated 180° to avoid overlap, but in this case, any azimuths measured from the back hemisphere must be corrected.
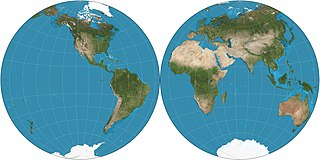
The Nicolosi globular projection is a polyconic map projection invented about the year 1,000 by the Iranian polymath al-Biruni. As a circular representation of a hemisphere, it is called globular because it evokes a globe. It can only display one hemisphere at a time and so normally appears as a "double hemispheric" presentation in world maps. The projection came into use in the Western world starting in 1660, reaching its most common use in the 19th century. As a "compromise" projection, it preserves no particular properties, instead giving a balance of distortions.
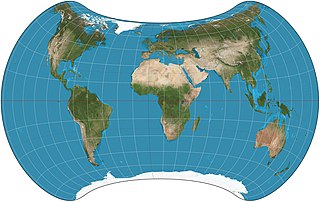
The Strebe 1995 projection, Strebe projection, Strebe lenticular equal-area projection, or Strebe equal-area polyconic projection is an equal-area map projection presented by Daniel "daan" Strebe in 1994. Strebe designed the projection to keep all areas proportionally correct in size; to push as much of the inevitable distortion as feasible away from the continental masses and into the Pacific Ocean; to keep a familiar equatorial orientation; and to do all this without slicing up the map.
The Eckert-Greifendorff projection is an equal-area map projection described by Max Eckert-Greifendorff in 1935. Unlike his previous six projections, it is not pseudocylindrical.























