
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In physics, the CHSH inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden-variable theories. Experimental verification of the inequality being violated is seen as confirmation that nature cannot be described by such theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969. They derived the CHSH inequality, which, as with John Stewart Bell's original inequality, is a constraint—on the statistical occurrence of "coincidences" in a Bell test—which is necessarily true if an underlying local hidden-variable theory exists. In practice, the inequality is routinely violated by modern experiments in quantum mechanics.
In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.
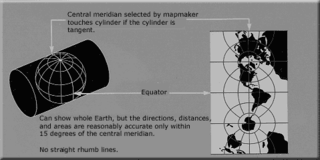
The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercator. When paired with a suitable geodetic datum, the transverse Mercator delivers high accuracy in zones less than a few degrees in east-west extent.

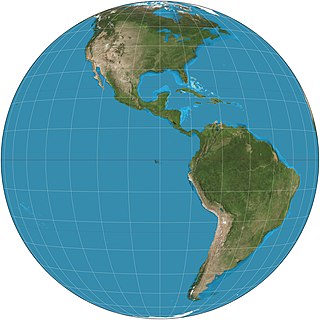
Orthographic projection in cartography has been used since antiquity. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic projection is at infinite distance. It depicts a hemisphere of the globe as it appears from outer space, where the horizon is a great circle. The shapes and areas are distorted, particularly near the edges.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians as straight, with distances from the pole represented correctly.

The scale of a map is the ratio of a distance on the map to the corresponding distance on the ground. This simple concept is complicated by the curvature of the Earth's surface, which forces scale to vary across a map. Because of this variation, the concept of scale becomes meaningful in two distinct ways.
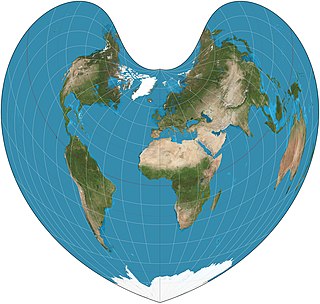
The Bonne projection is a pseudoconical equal-area map projection, sometimes called a dépôt de la guerre, modified Flamsteed, or a Sylvanus projection. Although named after Rigobert Bonne (1727–1795), the projection was in use prior to his birth, in 1511 by Sylvanus, Honter in 1561, De l'Isle before 1700 and Coronelli in 1696. Both Sylvanus and Honter's usages were approximate, however, and it is not clear they intended to be the same projection.
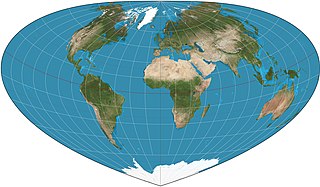
The Bottomley map projection is a pseudoconical equal area map projection defined as:

In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.
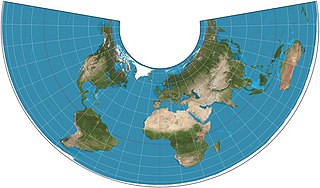
The Albers equal-area conic projection, or Albers projection, is a conic, equal area map projection that uses two standard parallels. Although scale and shape are not preserved, distortion is minimal between the standard parallels.
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as . Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential.
The General Perspective projection is a map projection. When the Earth is photographed from space, the camera records the view as a perspective projection. When the camera is aimed toward the center of the Earth, the resulting projection is called Vertical Perspective. When aimed in other directions, the resulting projection is called a Tilted Perspective.
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:
In mathematics, log-polar coordinates is a coordinate system in two dimensions, where a point is identified by two numbers, one for the logarithm of the distance to a certain point, and one for an angle. Log-polar coordinates are closely connected to polar coordinates, which are usually used to describe domains in the plane with some sort of rotational symmetry. In areas like harmonic and complex analysis, the log-polar coordinates are more canonical than polar coordinates.

The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west.
Transverse Mercator projection has many implementations. Louis Krüger in 1912 developed one of his two implementations that expressed as a power series in the longitude difference from the central meridian. These series were recalculated by Lee in 1946, by Redfearn in 1948, and by Thomas in 1952. They are often referred to as the Redfearn series, or the Thomas series. This implementation is of great importance since it is widely used in the U.S. State Plane Coordinate System, in national and also international mapping systems, including the Universal Transverse Mercator coordinate system (UTM). They are also incorporated into the Geotrans coordinate converter made available by the United States National Geospatial-Intelligence Agency. When paired with a suitable geodetic datum, the series deliver high accuracy in zones less than a few degrees in east-west extent.

In the cartography of the United States, the American polyconic projection is a map projection used for maps of the United States and its regions beginning early in the 19th century. It belongs to the polyconic projection class, which consists of map projections whose parallels are non-concentric circular arcs except for the equator, which is straight. Often the American polyconic is simply called the polyconic projection.





















