Richard Buckminster Fuller was an American architect, systems theorist, writer, designer, inventor, philosopher, and futurist. He styled his name as R. Buckminster Fuller in his writings, publishing more than 30 books and coining or popularizing such terms as "Spaceship Earth", "Dymaxion", "ephemeralization", "synergetics", and "tensegrity".

In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.

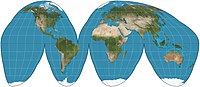
The Dymaxion map or Fuller map is a projection of a world map onto the surface of an icosahedron, which can be unfolded and flattened to two dimensions. The flat map is heavily interrupted in order to preserve shapes and sizes.

The Dymaxion car was designed by American inventor Buckminster Fuller during the Great Depression and featured prominently at Chicago's 1933/1934 World's Fair. Fuller built three experimental prototypes with naval architect Starling Burgess – using donated money as well as a family inheritance – to explore not an automobile per se, but the 'ground-taxiing phase' of a vehicle that might one day be designed to fly, land and drive – an "Omni-Medium Transport". Fuller associated the word Dymaxion with much of his work, a portmanteau of the words dynamic, maximum, and tension, to summarize his goal to do more with less.

The Robinson projection is a map projection of a world map that shows the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image.

A world map is a map of most or all of the surface of Earth. World maps, because of their scale, must deal with the problem of projection. Maps rendered in two dimensions by necessity distort the display of the three-dimensional surface of the earth. While this is true of any map, these distortions reach extremes in a world map. Many techniques have been developed to present world maps that address diverse technical and aesthetic goals.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The Goode homolosine projection is a pseudocylindrical, equal-area, composite map projection used for world maps. Normally it is presented with multiple interruptions. Its equal-area property makes it useful for presenting spatial distribution of phenomena.
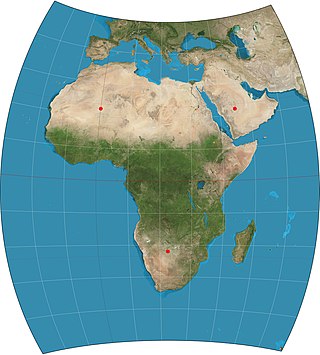
The Chamberlin trimetric projection is a map projection where three points are fixed on the globe and the points on the sphere are mapped onto a plane by triangulation. It was developed in 1946 by Wellman Chamberlin for the National Geographic Society. Chamberlin was chief cartographer for the Society from 1964 to 1971. The projection's principal feature is that it compromises between distortions of area, direction, and distance. A Chamberlin trimetric map therefore gives an excellent overall sense of the region being mapped. Many National Geographic Society maps of single continents use this projection.

Bernard Joseph Stanislaus Cahill, American cartographer and architect, was the inventor of the octahedral "Butterfly Map". An early proponent of the San Francisco Civic Center, he also designed hotels, factories and mausoleums like the Columbarium of San Francisco.

The Geoscope was a proposal by Buckminster Fuller around 1960 to create a 200-foot-diameter (61 m) globe that would be covered in colored lights so that it could function as a large spherical display. It was envisioned that the Geoscope would be connected to computers which would allow it to display both historical and current data, and enable people to visualize large scale patterns around the world. Several projects by his students to build a "miniature Earth", starting with a 20-foot version at Cornell University in 1952, were precursors of the Geoscope proposal. Before proposing the Geoscope, Fuller had invented the Dymaxion map, a novel map projection for the whole Earth.

The Waterman "Butterfly" World Map is a map projection created by Steve Waterman. Waterman first published a map in this arrangement in 1996. The arrangement is an unfolding of a polyhedral globe with the shape of a truncated octahedron, evoking the butterfly map principle first developed by Bernard J.S. Cahill (1866–1944) in 1909. Cahill and Waterman maps can be shown in various profiles, typically linked at the north Pacific or north Atlantic oceans.

The Cahill–Keyes projection is a polyhedral compromise map projection first proposed by Gene Keyes in 1975. The projection is a refinement of an earlier 1909 projection by Bernard Cahill. The projection was designed to achieve a number of desirable characteristics, namely symmetry of component maps (octants), scalability allowing the map to continue to work well even at high resolution, uniformity of geocells, metric-based joining edges, minimized distortion compared to a globe, and an easily understood orientation to enhance general usability and teachability.

The Boggs eumorphic projection is a pseudocylindrical, equal-area map projection used for world maps. Normally it is presented with multiple interruptions. Its equal-area property makes it useful for presenting spatial distribution of phenomena. The projection was developed in 1929 by Samuel Whittemore Boggs (1889–1954) to provide an alternative to the Mercator projection for portraying global areal relationships. Boggs was geographer for the United States Department of State from 1924 until his death. The Boggs eumorphic projection has been used occasionally in textbooks and atlases.
Hajime Narukawa is a Japanese architect. He was born in 1971 in Kawasaki, Kanagawa and lives and practices in Tokyo.

The octant projection or octants projection, is a type of map projection proposed the first time, in 1508, by Leonardo da Vinci in his Codex Atlanticus. Leonardo's authorship would be demonstrated by Christopher Tyler, who stated "For those projections dated later than 1508, his drawings should be effectively considered the original precursors..".

Gene Scott Keyes is a former Assistant Professor of World Politics, a sometime peace activist, noted cartographer, and promoter of the international second language Esperanto. He achieved considerable attention for his peace activism when his mother, Charlotte E. Keyes wrote an article for McCall's, Suppose They Gave a War and Nobody Came. The title phrase, based on a quote from a Carl Sandburg poem, became part of the anti-Vietnam-War lexicon. The slogan also went on to become the basis of the film Suppose They Gave a War and Nobody Came. His cartography work has won two awards.

In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped.

A polyhedral map projection is a map projection based on a spherical polyhedron. Typically, the polyhedron is overlaid on the globe, and each face of the polyhedron is transformed to a polygon or other shape in the plane. The best-known polyhedral map projection is Buckminster Fuller's Dymaxion map. When the spherical polyhedron faces are transformed to the faces of an ordinary polyhedron instead of laid flat in a plane, the result is a polyhedral globe.