
An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.

The haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes. Important in navigation, it is a special case of a more general formula in spherical trigonometry, the law of haversines, that relates the sides and angles of spherical triangles.
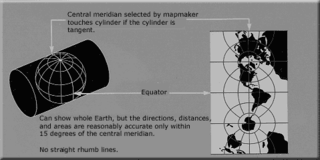
The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercator. When paired with a suitable geodetic datum, the transverse Mercator delivers high accuracy in zones less than a few degrees in east-west extent.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians as straight, with distances from the pole represented correctly.
The Bonne projection is a pseudoconical equal-area map projection, sometimes called a dépôt de la guerre, modified Flamsteed, or a Sylvanus projection. Although named after Rigobert Bonne (1727–1795), the projection was in use prior to his birth, by Sylvanus in 1511, Honter in 1561, De l'Isle before 1700 and Coronelli in 1696. Both Sylvanus and Honter's usages were approximate, however, and it is not clear they intended to be the same projection.
The Bottomley map projection is a pseudoconical equal area map projection defined as:

In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.
The Albers equal-area conic projection, or Albers projection, is a conic, equal area map projection that uses two standard parallels. Although scale and shape are not preserved, distortion is minimal between the standard parallels.

The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide.

The Cassini projection is a map projection first described in an approximate form by César-François Cassini de Thury in 1745. Its precise formulas were found through later analysis by Johann Georg von Soldner around 1810. It is the transverse aspect of the equirectangular projection, in that the globe is first rotated so the central meridian becomes the "equator", and then the normal equirectangular projection is applied. Considering the earth as a sphere, the projection is composed of the operations:
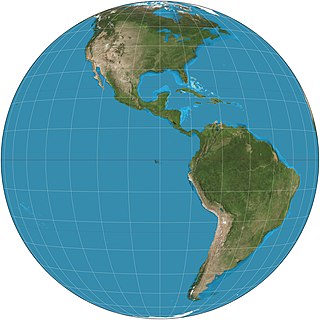
The General Perspective projection is a map projection. When the Earth is photographed from space, the camera records the view as a perspective projection. When the camera is aimed toward the center of the Earth, the resulting projection is called Vertical Perspective. When aimed in other directions, the resulting projection is called a Tilted Perspective.

Wagner VI is a pseudocylindrical whole Earth map projection. Like the Robinson projection, it is a compromise projection, not having any special attributes other than a pleasing, low distortion appearance. Wagner VI is equivalent to the Kavrayskiy VII horizontally elongated by a factor of ⁄. This elongation results in proper preservation of shapes near the equator but slightly more distortion overall. The aspect ratio of this projection is 2:1, as formed by the ratio of the equator to the central meridian. This matches the ratio of Earth’s equator to any meridian.

The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west.

The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III.

The armadillo projection is a map projection used for world maps. It is neither conformal nor equal-area but instead affords a view evoking a perspective projection while showing most of the globe instead of the half or less that a perspective would. The projection was presented in 1943 by Erwin Raisz (1893–1968) as part of a series of "orthoapsidal" projections, which are perspectives of the globe projected onto various surfaces. This entry in the series has the globe projected onto the outer half of half a torus. Raisz singled it out and named it the "armadillo" projection.
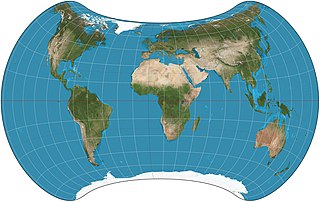
The Strebe 1995 projection, Strebe projection, Strebe lenticular equal-area projection, or Strebe equal-area polyconic projection is an equal-area map projection presented by Daniel "daan" Strebe in 1994. Strebe designed the projection to keep all areas proportionally correct in size; to push as much of the inevitable distortion as feasible away from the continental masses and into the Pacific Ocean; to keep a familiar equatorial orientation; and to do all this without slicing up the map.
The Eckert-Greifendorff projection is an equal-area map projection described by Max Eckert-Greifendorff in 1935. Unlike his previous six projections, it is not pseudocylindrical.
























