
In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth at a given latitude coordinate line.

The Robinson projection is a map projection of a world map that shows the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

The sinusoidal projection is a pseudocylindrical equal-area map projection, sometimes called the Sanson–Flamsteed or the Mercator equal-area projection. Jean Cossin of Dieppe was one of the first mapmakers to use the sinusoidal, using it in a world map in 1570.
The Collignon projection is an equal-area pseudocylindrical map projection first known to be published by Édouard Collignon in 1865 and subsequently cited by A. Tissot in 1881.

The Winkel tripel projection, a modified azimuthal map projection of the world, is one of three projections proposed by German cartographer Oswald Winkel in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection: The name tripel refers to Winkel's goal of minimizing three kinds of distortion: area, direction, and distance.

The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide.

The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections that may be used for world maps. Waldo R. Tobler introduced the construction in 1973 as the hyperelliptical projection, now usually known as the Tobler hyperelliptical projection.

The Kavrayskiy VII projection is a map projection invented by Soviet cartographer Vladimir V. Kavrayskiy in 1939 for use as a general-purpose pseudocylindrical projection. Like the Robinson projection, it is a compromise intended to produce good-quality maps with low distortion overall. It scores well in that respect compared to other popular projections, such as the Winkel tripel, despite straight, evenly spaced parallels and a simple formulation. Regardless, it has not been widely used outside the former Soviet Union.

Wagner VI is a pseudocylindrical whole Earth map projection. Like the Robinson projection, it is a compromise projection, not having any special attributes other than a pleasing, low distortion appearance. Wagner VI is equivalent to the Kavrayskiy VII horizontally elongated by a factor of ⁄. This elongation results in proper preservation of shapes near the equator but slightly more distortion overall. The aspect ratio of this projection is 2:1, as formed by the ratio of the equator to the central meridian. This matches the ratio of Earth’s equator to any meridian.

The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III.

The Eckert II projection is an equal-area pseudocylindrical map projection. In the equatorial aspect the network of longitude and latitude lines consists solely of straight lines, and the outer boundary has the distinctive shape of an elongated hexagon. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, the meridians have the same shape, and the odd-numbered projection has equally spaced parallels, whereas the even-numbered projection has parallels spaced to preserve area. The pair to Eckert II is the Eckert I projection.
The Eckert projections are six pseudocylindrical map projections devised by Max Eckert-Greifendorff, who presented them in 1906. The latitudes are parallel lines in all six projections. The projections come in pairs; in the odd-numbered projections, the latitudes are equally spaced, while their even-numbered counterparts are equal-area.

The Ortelius oval projection is a map projection used for world maps largely in the late 16th and early 17th century. It is neither conformal nor equal-area but instead offers a compromise presentation. It is similar in structure to a pseudocylindrical projection but does not qualify as one because the meridians are not equally spaced along the parallels. The projection's first known use was by Battista Agnese around 1540, although whether the construction method was truly identical to Ortelius's or not is unclear because of crude drafting and printing. The front hemisphere is identical to Petrus Apianus's 1524 globular projection.
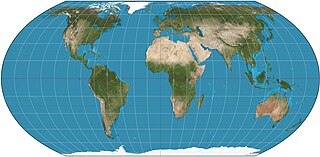
The Equal Earth map projection is an equal-area pseudocylindrical global map projection, invented by Bojan Šavrič, Bernhard Jenny, and Tom Patterson in 2018. It is inspired by the widely used Robinson projection, but unlike the Robinson projection, retains the relative size of areas. The projection equations are simple to implement and fast to evaluate.

In map projections, an interruption is any place where the globe has been split. All map projections are interrupted at at least one point. Typical world maps are interrupted along an entire meridian. In that typical case, the interruption forms an east/west boundary, even though the globe has no boundaries.
The Eckert-Greifendorff projection is an equal-area map projection described by Max Eckert-Greifendorff in 1935. Unlike his previous six projections, it is not pseudocylindrical.

In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped.















