Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor.

JPEG is a commonly used method of lossy compression for digital images, particularly for those images produced by digital photography. The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality. Since its introduction in 1992, JPEG has been the most widely used image compression standard in the world, and the most widely used digital image format, with several billion JPEG images produced every day as of 2015.

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
A video codec is software or hardware that compresses and decompresses digital video. In the context of video compression, codec is a portmanteau of encoder and decoder, while a device that only compresses is typically called an encoder, and one that only decompresses is a decoder.

JPEG 2000 (JP2) is an image compression standard and coding system. It was developed from 1997 to 2000 by a Joint Photographic Experts Group committee chaired by Touradj Ebrahimi, with the intention of superseding their original JPEG standard, which is based on a discrete cosine transform (DCT), with a newly designed, wavelet-based method. The standardized filename extension is .jp2 for ISO/IEC 15444-1 conforming files and .jpx for the extended part-2 specifications, published as ISO/IEC 15444-2. The registered MIME types are defined in RFC 3745. For ISO/IEC 15444-1 it is image/jp2.
ICER is a wavelet-based image compression file format used by the NASA Mars rovers. ICER has both lossy and lossless compression modes.
The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.
Set partitioning in hierarchical trees (SPIHT) is an image compression algorithm that exploits the inherent similarities across the subbands in a wavelet decomposition of an image. The algorithm was developed by Brazilian engineer Amir Said with William A. Pearlman in 1996.
Originally known as optimal subband tree structuring (SB-TS), also called wavelet packet decomposition (WPD) (sometimes known as just wavelet packets or subband tree), is a wavelet transform where the discrete-time (sampled) signal is passed through more filters than the discrete wavelet transform (DWT).
The Stationary wavelet transform (SWT) is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of in the th level of the algorithm. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input – so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as "algorithme à trous" in French which refers to inserting zeros in the filters. It was introduced by Holschneider et al.

Cohen–Daubechies–Feauveau wavelets are a family of biorthogonal wavelets that was made popular by Ingrid Daubechies. These are not the same as the orthogonal Daubechies wavelets, and also not very similar in shape and properties. However, their construction idea is the same.

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.
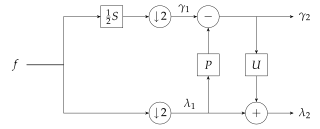
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.

PGF is a wavelet-based bitmapped image format that employs lossless and lossy data compression. PGF was created to improve upon and replace the JPEG format. It was developed at the same time as JPEG 2000 but with a focus on speed over compression ratio.
Ali Naci Akansu is a Turkish-American Professor of electrical & computer engineering and scientist in applied mathematics.
Wavelets are often used to analyse piece-wise smooth signals. Wavelet coefficients can efficiently represent a signal which has led to data compression algorithms using wavelets. Wavelet analysis is extended for multidimensional signal processing as well. This article introduces a few methods for wavelet synthesis and analysis for multidimensional signals. There also occur challenges such as directivity in multidimensional case.
JPEG XS is an interoperable, visually lossless, low-latency and lightweight image and video coding system used in professional applications. Applications of the standard include streaming high quality content for virtual reality, drones, autonomous vehicles using cameras, gaming, and broadcasting. In this respect, JPEG XS is unique, being the first ISO codec ever designed for this specific purpose. JPEG XS, built on core technology from both intoPIX and Fraunhofer IIS, is formally standardized as ISO/IEC 21122 by the Joint Photographic Experts Group with the first edition published in 2019. Although not official, the XS acronym was chosen to highlight the eXtra Small and eXtra Speed characteristics of the codec. Today, the JPEG committee is still actively working on further improvements to XS, with the second edition scheduled for publication and initial efforts being launched towards a third edition.
In applied mathematics, biorthogonal nearly coiflet bases are wavelet bases proposed by Lowell L. Winger. The wavelet is based on biorthogonal coiflet wavelet bases, but sacrifices its regularity to increase the filter's bandwidth, which might lead to better image compression performance.





