
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".

In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable , which takes values in the alphabet and is distributed according to :

JPEG is a commonly used method of lossy compression for digital images, particularly for those images produced by digital photography. The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality. Since its introduction in 1992, JPEG has been the most widely used image compression standard in the world, and the most widely used digital image format, with several billion JPEG images produced every day as of 2015.
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency carrier wave. The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication.
In information theory, an entropy coding is any lossless data compression method that attempts to approach the lower bound declared by Shannon's source coding theorem, which states that any lossless data compression method must have expected code length greater or equal to the entropy of the source.
Elias code or Elias gamma code is a universal code encoding positive integers developed by Peter Elias. It is used most commonly when coding integers whose upper-bound cannot be determined beforehand.

Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a string of characters is represented using a fixed number of bits per character, as in the ASCII code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding, such as Huffman coding, in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, an arbitrary-precision fraction q, where 0.0 ≤ q < 1.0. It represents the current information as a range, defined by two numbers. A recent family of entropy coders called asymmetric numeral systems allows for faster implementations thanks to directly operating on a single natural number representing the current information.
In mathematics, a real number is said to be simply normal in an integer base b if its infinite sequence of digits is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b. A number is said to be normal in base b if, for every positive integer n, all possible strings n digits long have density b−n.
Unary coding, or the unary numeral system and also sometimes called thermometer code, is an entropy encoding that represents a natural number, n, with a code of length n + 1, usually n ones followed by a zero or with n − 1 ones followed by a zero. For example 5 is represented as 111110 or 11110. Some representations use n or n − 1 zeros followed by a one. The ones and zeros are interchangeable without loss of generality. Unary coding is both a prefix-free code and a self-synchronizing code.
Truncated binary encoding is an entropy encoding typically used for uniform probability distributions with a finite alphabet. It is parameterized by an alphabet with total size of number n. It is a slightly more general form of binary encoding when n is not a power of two.
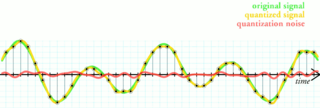
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms.
Elias ω coding or Elias omega coding is a universal code encoding the positive integers developed by Peter Elias. Like Elias gamma coding and Elias delta coding, it works by prefixing the positive integer with a representation of its order of magnitude in a universal code. Unlike those other two codes, however, Elias omega recursively encodes that prefix; thus, they are sometimes known as recursive Elias codes.

In data compression, a universal code for integers is a prefix code that maps the positive integers onto binary codewords, with the additional property that whatever the true probability distribution on integers, as long as the distribution is monotonic (i.e., p(i) ≥ p(i + 1) for all positive i), the expected lengths of the codewords are within a constant factor of the expected lengths that the optimal code for that probability distribution would have assigned. A universal code is asymptotically optimal if the ratio between actual and optimal expected lengths is bounded by a function of the information entropy of the code that, in addition to being bounded, approaches 1 as entropy approaches infinity.
Lossless JPEG is a 1993 addition to JPEG standard by the Joint Photographic Experts Group to enable lossless compression. However, the term may also be used to refer to all lossless compression schemes developed by the group, including JPEG 2000 and JPEG-LS.
FELICS, which stands for Fast Efficient & Lossless Image Compression System, is a lossless image compression algorithm that performs 5-times faster than the original lossless JPEG codec and achieves a similar compression ratio.
An exponential-Golomb code is a type of universal code. To encode any nonnegative integer x using the exp-Golomb code:
- Write down x+1 in binary
- Count the bits written, subtract one, and write that number of starting zero bits preceding the previous bit string.

PGF is a wavelet-based bitmapped image format that employs lossless and lossy data compression. PGF was created to improve upon and replace the JPEG format. It was developed at the same time as JPEG 2000 but with a focus on speed over compression ratio.
Distributed source coding (DSC) is an important problem in information theory and communication. DSC problems regard the compression of multiple correlated information sources that do not communicate with each other. By modeling the correlation between multiple sources at the decoder side together with channel codes, DSC is able to shift the computational complexity from encoder side to decoder side, therefore provide appropriate frameworks for applications with complexity-constrained sender, such as sensor networks and video/multimedia compression. One of the main properties of distributed source coding is that the computational burden in encoders is shifted to the joint decoder.
In cryptography, Very Smooth Hash (VSH) is a provably secure cryptographic hash function invented in 2005 by Scott Contini, Arjen Lenstra and Ron Steinfeld. Provably secure means that finding collisions is as difficult as some known hard mathematical problem. Unlike other provably secure collision-resistant hashes, VSH is efficient and usable in practice. Asymptotically, it only requires a single multiplication per log(n) message-bits and uses RSA-type arithmetic. Therefore, VSH can be useful in embedded environments where code space is limited.
Asymmetric numeral systems (ANS) is a family of entropy encoding methods introduced by Jarosław (Jarek) Duda from Jagiellonian University, used in data compression since 2014 due to improved performance compared to previous methods. ANS combines the compression ratio of arithmetic coding, with a processing cost similar to that of Huffman coding. In the tabled ANS (tANS) variant, this is achieved by constructing a finite-state machine to operate on a large alphabet without using multiplication.












































