
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. They belong to the class of convex uniform polyhedra, the convex polyhedra with regular faces and symmetric vertices, which is divided into the Archimedean solids, the five Platonic solids, and the two infinite families of prisms and antiprisms. The pseudorhombicuboctahedron is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. An even larger class than the convex uniform polyhedra is the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, the regular icosahedron is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a strictly convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two solids with such a property: the first solids are the pyramids, cupolas. and a rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. These solids are named after mathematicians Norman Johnson and Victor Zalgaller.
In geometry, an octahedron is a polyhedron with eight faces. An octahedron can be considered as a square bipyramid. When the edges of a square bipyramid are all equal in length, it produces a regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. It is also an example of a deltahedron. An octahedron is the three-dimensional case of the more general concept of a cross polytope.

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.

In geometry, a deltahedron is a polyhedron whose faces are all (congruent) equilateral triangles. The name is taken from the Greek upper case delta letter (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra. By the handshaking lemma, each deltahedron has an even number of faces. Only eight deltahedra are strictly convex; these have 4, 6, 8, 10, 12, 14, 16, and 20 faces. These eight deltahedra, with their respective numbers of faces, edges, and vertices, are listed below.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid, with 60 isosceles triangle faces. Its dual is the truncated dodecahedron. It has also been called the kisicosahedron. It was first depicted, in a non-convex form with equilateral triangle faces, by Leonardo da Vinci in Luca Pacioli's Divina proportione, where it was named the icosahedron elevatum. The capsid of the Hepatitis A virus has the shape of a triakis icosahedron.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. Many polyhedrons can be constructed involving the attachment of the base of a triangular cupola.

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.
In geometry, a snub polyhedron is a polyhedron obtained by performing a snub operation: alternating a corresponding omnitruncated or truncated polyhedron, depending on the definition. Some, but not all, authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
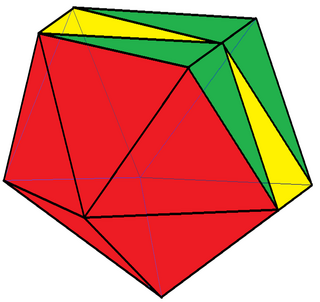
In geometry, an edge-contracted icosahedron is a polyhedron with 18 triangular faces, 27 edges, and 11 vertices.
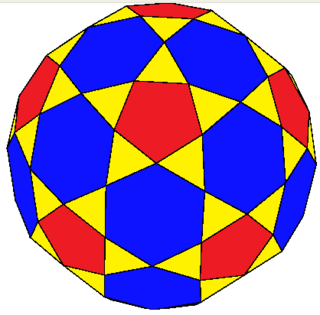
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.

In geometry, the ten-of-diamonds decahedron is a space-filling polyhedron with 10 faces, 2 opposite rhombi with orthogonal major axes, connected by 8 identical isosceles triangle faces. Although it is convex, it is not a Johnson solid because its faces are not composed entirely of regular polygons. Michael Goldberg named it after a playing card, as a 10-faced polyhedron with two opposite rhombic (diamond-shaped) faces. He catalogued it in a 1982 paper as 10-II, the second in a list of 26 known space-filling decahedra.



















