
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number x. In the simplest case, the logarithm counts the number of occurrences of the same factor in repeated multiplication; e.g., since 1000 = 10 × 10 × 10 = 103, the "logarithm base 10" of 1000 is 3, or log10(1000) = 3. The logarithm of x to baseb is denoted as logb(x), or without parentheses, logb x, or even without the explicit base, log x, when no confusion is possible, or when the base does not matter such as in big O notation.

Benford's law, also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30 % of the time, while 9 appears as the leading significant digit less than 5 % of the time. If the digits were distributed uniformly, they would each occur about 11.1 % of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

Information geometry is an interdisciplinary field that applies the techniques of differential geometry to study probability theory and statistics. It studies statistical manifolds, which are Riemannian manifolds whose points correspond to probability distributions.
In statistics, the generalized linear model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola, to hyperbole, or to hyperbolic geometry.

In mathematics, a hyperbolic angle is a geometric figure that defines a hyperbolic sector. The relationship of a hyperbolic angle to a hyperbola parallels the relationship of an "ordinary" angle to a circle.
In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave if its domain is a convex set, and if it satisfies the inequality

Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in logic. In philosophical logic, Martin-Löf has wrestled with the philosophy of logical consequence and judgment, partly inspired by the work of Brentano, Frege, and Husserl. In mathematical logic, Martin-Löf has been active in developing intuitionistic type theory as a constructive foundation of mathematics; Martin-Löf's work on type theory has influenced computer science.
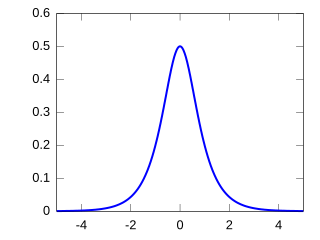
In probability theory and statistics, the hyperbolic secant distribution is a continuous probability distribution whose probability density function and characteristic function are proportional to the hyperbolic secant function. The hyperbolic secant function is equivalent to the reciprocal hyperbolic cosine, and thus this distribution is also called the inverse-cosh distribution.

Grégoire de Saint-Vincent was a Flemish Jesuit and mathematician. He is remembered for his work on quadrature of the hyperbola.

In probability theory and statistics, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distributions with probability density function
The generalised hyperbolic distribution (GH) is a continuous probability distribution defined as the normal variance-mean mixture where the mixing distribution is the generalized inverse Gaussian distribution (GIG). Its probability density function is given in terms of modified Bessel function of the second kind, denoted by . It was introduced by Ole Barndorff-Nielsen, who studied it in the context of physics of wind-blown sand.

Ole Eiler Barndorff-Nielsen is a Danish statistician who has contributed to many areas of statistical science.
In probability theory and statistics, a normal variance-mean mixture with mixing probability density is the continuous probability distribution of a random variable of the form
The normal-inverse Gaussian distribution (NIG) is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.
The variance-gamma distribution, generalized Laplace distribution or Bessel function distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the gamma distribution. The tails of the distribution decrease more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The distribution was introduced in the financial literature by Madan and Seneta. The variance-gamma distributions form a subclass of the generalised hyperbolic distributions.

The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation until the advent of the digital computer. The Napierian logarithms were published first in 1614. Henry Briggs introduced common logarithms, which were easier to use. Tables of logarithms were published in many forms over four centuries. The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s. A breakthrough generating the natural logarithm was the result of a search for an expression of area against a rectangular hyperbola, and required the assimilation of a new function into standard mathematics.

Introductio in analysin infinitorum is a two-volume work by Leonhard Euler which lays the foundations of mathematical analysis. Written in Latin and published in 1748, the Introductio contains 18 chapters in the first part and 22 chapters in the second. It has Eneström numbers E101 and E102.
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive beyond any specified time.






















