
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable , or just distribution function of , evaluated at , is the probability that will take a value less than or equal to .

In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.

In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by , , , , or .
In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the distribution of a normalized version of the sample mean converges to a standard normal distribution. This holds even if the original variables themselves are not normally distributed. There are several versions of the CLT, each applying in the context of different conditions.
In probability theory, Chebyshev's inequality provides an upper bound on the probability of deviation of a random variable from its mean. More specifically, the probability that a random variable deviates from its mean by more than is at most , where is any positive constant and is the standard deviation.
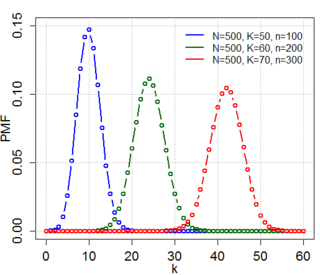
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.
In probability theory, the central limit theorem states that, under certain circumstances, the probability distribution of the scaled mean of a random sample converges to a normal distribution as the sample size increases to infinity. Under stronger assumptions, the Berry–Esseen theorem, or Berry–Esseen inequality, gives a more quantitative result, because it also specifies the rate at which this convergence takes place by giving a bound on the maximal error of approximation between the normal distribution and the true distribution of the scaled sample mean. The approximation is measured by the Kolmogorov–Smirnov distance. In the case of independent samples, the convergence rate is n−1/2, where n is the sample size, and the constant is estimated in terms of the third absolute normalized moment.
In probability theory, a Chernoff bound is an exponentially decreasing upper bound on the tail of a random variable based on its moment generating function. The minimum of all such exponential bounds forms the Chernoff or Chernoff-Cramér bound, which may decay faster than exponential. It is especially useful for sums of independent random variables, such as sums of Bernoulli random variables.
In probability theory, Hoeffding's inequality provides an upper bound on the probability that the sum of bounded independent random variables deviates from its expected value by more than a certain amount. Hoeffding's inequality was proven by Wassily Hoeffding in 1963.
Students of statistics and probability theory sometimes develop misconceptions about the normal distribution, ideas that may seem plausible but are mathematically untrue. For example, it is sometimes mistakenly thought that two linearly uncorrelated, normally distributed random variables must be statistically independent. However, this is untrue, as can be demonstrated by counterexample. Likewise, it is sometimes mistakenly thought that a linear combination of normally distributed random variables will itself be normally distributed, but again, counterexamples prove this wrong.
In probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound.

In the theory of probability and statistics, the Dvoretzky–Kiefer–Wolfowitz–Massart inequality provides a bound on the worst case distance of an empirically determined distribution function from its associated population distribution function. It is named after Aryeh Dvoretzky, Jack Kiefer, and Jacob Wolfowitz, who in 1956 proved the inequality
In probability theory, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive ,
In mathematics, the second moment method is a technique used in probability theory and analysis to show that a random variable has positive probability of being positive. More generally, the "moment method" consists of bounding the probability that a random variable fluctuates far from its mean, by using its moments.
In probability theory, the multidimensional Chebyshev's inequality is a generalization of Chebyshev's inequality, which puts a bound on the probability of the event that a random variable differs from its expected value by more than a specified amount.
In probability theory and statistics, the Poisson binomial distribution is the discrete probability distribution of a sum of independent Bernoulli trials that are not necessarily identically distributed. The concept is named after Siméon Denis Poisson.
In probability theory, concentration inequalities provide mathematical bounds on the probability of a random variable deviating from some value.
For certain applications in linear algebra, it is useful to know properties of the probability distribution of the largest eigenvalue of a finite sum of random matrices. Suppose is a finite sequence of random matrices. Analogous to the well-known Chernoff bound for sums of scalars, a bound on the following is sought for a given parameter t:
In probability theory, Eaton's inequality is a bound on the largest values of a linear combination of bounded random variables. This inequality was described in 1974 by Morris L. Eaton.
In probability theory, a subgaussian distribution, the distribution of a subgaussian random variable, is a probability distribution with strong tail decay. More specifically, the tails of a subgaussian distribution are dominated by the tails of a Gaussian. This property gives subgaussian distributions their name.

























