Icosioctagon

Last updated
Regular icosioctagon
Regular polygon 28.svg
A regular icosioctagon
Type Regular polygon
Edges and vertices 28
Schläfli symbol {28}, t{14}
Coxeter–Dynkin diagrams CDel node 1.pngCDel 2x.pngCDel 8.pngCDel node.png
CDel node 1.pngCDel 14.pngCDel node 1.png
Symmetry group Dihedral (D28), order 2×28
Internal angle (degrees)≈167.143°
Properties Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, an icosioctagon (or icosikaioctagon) or 28-gon is a twenty eight sided polygon. The sum of any icosioctagon's interior angles is 4680 degrees.

Contents

Regular icosioctagon

The regular icosioctagon is represented by Schläfli symbol {28} and can also be constructed as a truncated tetradecagon, t{14}, or a twice-truncated heptagon, tt{7}.

The area of a regular icosioctagon(28 sided polygon) is: (with t = edge length)

Construction

As 28 = 22 × 7, the icosioctagon is not constructible with a compass and straightedge, since 7 is not a Fermat prime. However, it can be constructed with an angle trisector, because 7 is a Pierpont prime.

Symmetry

The regular icosioctagon has Dih28 symmetry, order 56. There are 5 subgroup dihedral symmetries: (Dih14, Dih7), and (Dih4, Dih2, and Dih1), and 6 cyclic group symmetries: (Z28, Z14, Z7), and (Z4, Z2, Z1).

These 10 symmetries can be seen in 16 distinct symmetries on the icosioctagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. [1] The full symmetry of the regular form is r56 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g28 subgroup has no degrees of freedom but can seen as directed edges.

The highest symmetry irregular icosioctagons are d28, an isogonal icosioctagon constructed by ten mirrors which can alternate long and short edges, and p28, an isotoxal icosioctagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular icosioctagon.

Dissection

28-gon with 364 rhombs
28-gon rhombic dissection-size2.svg
regular		 Isotoxal 28-gon rhombic dissection-size2.svg
Isotoxal

Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m − 1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular icosioctagon, m = 14, and it can be divided into 91: 7 squares and 6 sets of 14 rhombs. This decomposition is based on a Petrie polygon projection of a 14-cube. [2]

Examples
28-gon rhombic dissection.svg 28-gon rhombic dissection2.svg 28-gon-dissection-random.svg

An icosioctagram is a 28-sided star polygon. There are 5 regular forms given by Schläfli symbols: {28/3}, {28/5}, {28/9}, {28/11} and {28/13}.

Regular star polygon 28-3.svg
{28/3}		 Regular star polygon 28-5.svg
{28/5}		 Regular star polygon 28-9.svg
{28/9}		 Regular star polygon 28-11.svg
{28/11}		 Regular star polygon 28-13.svg
{28/13}

There are also isogonal icosioctagrams constructed as deeper truncations of the regular tetradecagon {14} and tetradecagrams {28/3}, {28/5}, {28/9}, and {28/11}. [3]

Related Research Articles

Icosagon Polygon with 20 edges

In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.

Triacontagon Polygon with 30 edges

In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.

Pentacontagon Polygon with 50 edges

In geometry, a pentacontagon or pentecontagon or 50-gon is a fifty-sided polygon. The sum of any pentacontagon's interior angles is 8640 degrees.

Hectogon Polygon with 100 edges

In geometry, a hectogon or hecatontagon or 100-gon is a hundred-sided polygon. The sum of all hectogon's interior angles are 17640 degrees.

Tetradecagon Polygon with 14 edges

In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.

Hexadecagon Polygon with 16 edges

In mathematics, a hexadecagon is a sixteen-sided polygon.

Octadecagon Polygon with 18 edges

In geometry, an octadecagon or 18-gon is an eighteen-sided polygon.

Icositetragon Polygon with 24 edges

In geometry, an icositetragon or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees.

Heptacontagon Polygon with 70 edges

In geometry, a heptacontagon or 70-gon is a seventy-sided polygon. The sum of any heptacontagon's interior angles is 12240 degrees.

Enneacontagon Polygon with 90 edges

In geometry, an enneacontagon or enenecontagon or 90-gon is a ninety-sided polygon. The sum of any enneacontagon's interior angles is 15840 degrees.

Triacontadigon Polygon with 32 edges

In geometry, a triacontadigon or 32-gon is a thirty-two-sided polygon. In Greek, the prefix triaconta- means 30 and di- means 2. The sum of any triacontadigon's interior angles is 5400 degrees.

Tetracontadigon Polygon with 42 edges

In geometry, a tetracontadigon or 42-gon is a forty-two-sided polygon. The sum of any tetracontadigon's interior angles is 7200 degrees.

Hexacontatetragon Polygon with 64 edges

In geometry, a hexacontatetragon or 64-gon is a sixty-four-sided polygon. The sum of any hexacontatetragon's interior angles is 11160 degrees.

Tetracontaoctagon Polygon with 48 edges

In geometry, a tetracontaoctagon or 48-gon is a forty-eight sided polygon. The sum of any tetracontaoctagon's interior angles is 8280 degrees.

Enneacontahexagon Polygon with 96 edges

In geometry, an enneacontahexagon or enneacontakaihexagon or 96-gon is a ninety-six-sided polygon. The sum of any enneacontahexagon's interior angles is 16920 degrees.

120-gon Polygon with 120 edges

In geometry, a 120-gon is a polygon with 120 sides. The sum of any 120-gon's interior angles is 21240 degrees.

360-gon

In geometry, a 360-gon is a polygon with 360 sides. The sum of any 360-gon's interior angles is 64440 degrees.

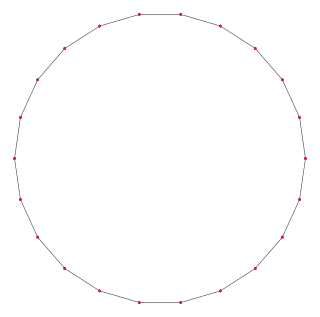
Icosidigon Polygon with 22 edges

In geometry, an icosidigon or 22-gon is a twenty-two-sided polygon. The sum of any icosidigon's interior angles is 360 degrees.

Icosihexagon Polygon with 26 edges

In geometry, an icosihexagon or 26-gon is a twenty-six-sided polygon. The sum of any icosihexagon's interior angles are 4320°.

Triacontatetragon Polygon with 34 edges

In geometry, a triacontatetragon or triacontakaitetragon is a thirty-four-sided polygon or 34-gon. The sum of any triacontatetragon's interior angles is 5760 degrees.

References

  1. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN   978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
  2. ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p. 141
  3. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.