In thermodynamics, the specific heat capacity of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity or as the specific heat. Informally, it is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−1⋅K−1.
In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.

The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form:

The kinetic theory of gases is a simple, historically significant classical model of the thermodynamic behavior of gases, with which many principal concepts of thermodynamics were established. The model describes a gas as a large number of identical submicroscopic particles, all of which are in constant, rapid, random motion. Their size is assumed to be much smaller than the average distance between the particles. The particles undergo random elastic collisions between themselves and with the enclosing walls of the container. The basic version of the model describes the ideal gas, and considers no other interactions between the particles.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.
In thermodynamics, the Joule–Thomson effect describes the temperature change of a real gas or liquid when it is forced through a valve or porous plug while keeping it insulated so that no heat is exchanged with the environment. This procedure is called a throttling process or Joule–Thomson process. At room temperature, all gases except hydrogen, helium, and neon cool upon expansion by the Joule–Thomson process when being throttled through an orifice; these three gases experience the same effect but only at lower temperatures. Most liquids such as hydraulic oils will be warmed by the Joule–Thomson throttling process.

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

The van der Waals equation, named for its originator, the Dutch physicist Johannes Diderik van der Waals, is an equation of state that extends the ideal gas law to include the non-zero size of gas molecules and the interactions between them. As a result the equation is able to model the phase change from liquid to gas, and vice versa. It also produces simple analytic expressions for the properties of real substances that shed light on their behavior. One common way to write this dimensional equation is:

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as

A thermodynamic potential is a scalar quantity used to represent the thermodynamic state of a system. Just as in mechanics, where potential energy is defined as capacity to do work, similarly different potentials have different meanings. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions.

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks

The internal energy of a thermodynamic system is the energy contained within it, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, i.e., the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. The internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics.
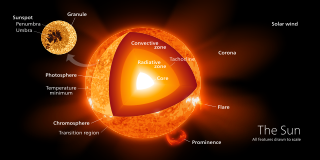
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions. This simple model can be used to describe the classical ideal gas as well as the various quantum ideal gases such as the ideal massive Fermi gas, the ideal massive Bose gas as well as black body radiation which may be treated as a massless Bose gas, in which thermalization is usually assumed to be facilitated by the interaction of the photons with an equilibrated mass.

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.
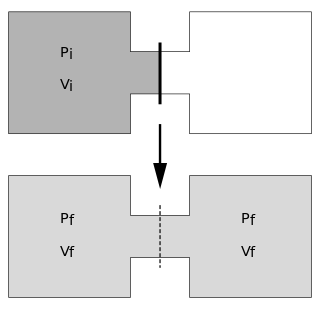
The Joule expansion is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container, with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container.
In nonideal fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845.
The Herschel–Bulkley fluid is a generalized model of a non-Newtonian fluid, in which the strain experienced by the fluid is related to the stress in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress . The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.






















































