| Figure | Definitions | Images |
|---|
| Parallelepiped | |  |
| Rhombohedron | | 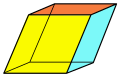 |
| Cuboid | |  |
| Polyhedron | Flat polygonal faces, straight edges and sharp corners or vertices | 
Small stellated dodecahedron | 
Toroidal polyhedron |
| Uniform polyhedron | Regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other) |  
(Regular)
Tetrahedron and Cube | 
Uniform
Snub dodecahedron |
| Pyramid | A polyhedron comprising an n-sided polygonal base and a vertex point | 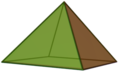 square pyramid square pyramid |
| Prism | A polyhedron comprising an n-sided polygonal base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases | 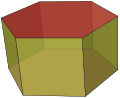 hexagonal prism hexagonal prism |
| Antiprism | A polyhedron comprising an n-sided polygonal base, a second base translated and rotated.sides]] of the two bases |  square antiprism square antiprism |
| Bipyramid | A polyhedron comprising an n-sided polygonal center with two apexes. | 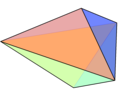 triangular bipyramid triangular bipyramid |
| Trapezohedron | A polyhedron with 2n kite faces around an axis, with half offsets |  tetragonal trapezohedron tetragonal trapezohedron |
| Cone | Tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex | 
A right circular cone and an oblique circular cone |
| Cylinder | Straight parallel sides and a circular or oval cross section | 
A solid elliptic cylinder | 
A right and an oblique circular cylinder |
| Ellipsoid | A surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation | 
Examples of ellipsoids | 
sphere (top, a=b=c=4),
spheroid (bottom left, a=b=5, c=3),
tri-axial ellipsoid (bottom right, a=4.5, b=6, c=3)]] |
| Lemon | A lens (or less than half of a circular arc) rotated about an axis passing through the endpoints of the lens (or arc) [6] |  |
| Hyperboloid | A surface that is generated by rotating a hyperbola around one of its principal axes |  |


















