Babylonian cuneiform numerals

Last updated
Babylonian cuneiform numerals Babylonian numerals.svg
Babylonian cuneiform numerals

Babylonian cuneiform numerals, also used in Assyria and Chaldea, were written in cuneiform, using a wedge-tipped reed stylus to print a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record.

Contents

The Babylonians, who were famous for their astronomical observations (Observations of the sky), as well as their calculations (aided by their invention of the abacus), used a sexagesimal (base-60) positional numeral system inherited from either the Sumerian or the Akkadian civilizations. [1] Neither of the predecessors was a positional system (having a convention for which 'end' of the numeral represented the units).

Origin

This system first appeared around 2000 BC; [1] its structure reflects the decimal lexical numerals of Semitic languages rather than Sumerian lexical numbers. [2] However, the use of a special Sumerian sign for 60 (beside two Semitic signs for the same number) [1] attests to a relation with the Sumerian system. [2]

Symbols

The Babylonian system is credited as being the first known positional numeral system, in which the value of a particular digit depends both on the digit itself and its position within the number. This was an extremely important development because non-place-value systems require unique symbols to represent each power of a base (ten, one hundred, one thousand, and so forth), which can make calculations more difficult.

Only two symbols ( Babylonian 1.svg to count units and Babylonian 10.svg to count tens) were used to notate the 59 non-zero digits. These symbols and their values were combined to form a digit in a sign-value notation quite similar to that of Roman numerals; for example, the combination Babylonian 20.svg Babylonian 3.svg represented the digit for 23 (see table of digits above).

These digits were used to represent larger numbers in the base 60 (sexagesimal) positional system. For example, Babylonian 2.svg   Babylonian 20.svg Babylonian 3.svg   Babylonian 3.svg would represent 2×602+23×60+3 = 8583.

A space was left to indicate a place without value, similar to the modern-day zero. Babylonians later devised a sign to represent this empty place. They lacked a symbol to serve the function of radix point, so the place of the units had to be inferred from context : Babylonian 20.svg Babylonian 3.svg could have represented 23 or 23×60 or 23×60×60 or 23/60, etc.

Their system clearly used internal decimal to represent digits, but it was not really a mixed-radix system of bases 10 and 6, since the ten sub-base was used merely to facilitate the representation of the large set of digits needed, while the place-values in a digit string were consistently 60-based and the arithmetic needed to work with these digit strings was correspondingly sexagesimal.

The legacy of sexagesimal still survives to this day, in the form of degrees (360° in a circle or 60° in an angle of an equilateral triangle), arcminutes, and arcseconds in trigonometry and the measurement of time, although both of these systems are actually mixed radix. [3]

A common theory is that 60, a superior highly composite number (the previous and next in the series being 12 and 120), was chosen due to its prime factorization: 2×2×3×5, which makes it divisible by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. Integers and fractions were represented identically—a radix point was not written but rather made clear by context.

Zero

The Babylonians did not technically have a digit for, nor a concept of, the number zero. Although they understood the idea of nothingness, it was not seen as a number—merely the lack of a number. Later Babylonian texts used a placeholder ( 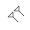Babylonian digit 0.svg ) to represent zero, but only in the medial positions, and not on the right-hand side of the number, as we do in numbers like 100. [4]

See also

Related Research Articles

In mathematics and computing, the hexadecimal numeral system is a positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbols, hexadecimal uses sixteen distinct symbols, most often the symbols "0"–"9" to represent values 0 to 9, and "A"–"F" to represent values from ten to fifteen.

<span class="mw-page-title-main">Numeral system</span> Notation for expressing numbers

A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.

<span class="mw-page-title-main">Number</span> Used to count, measure, and label

A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called numerals; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any non-negative integer using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels, for ordering, and for codes. In common usage, a numeral is not clearly distinguished from the number that it represents.

1 is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of unit length is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0.

0 (zero) is a number representing an empty quantity. Adding 0 to any number leaves that number unchanged. In mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Multiplying any number by 0 has the result 0, and consequently, division by zero has no meaning in arithmetic.

Sexagesimal, also known as base 60, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates.

A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero) and "1" (one).

A numerical digit is a single symbol used alone or in combinations, to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits of the hands correspond to the ten symbols of the common base 10 numeral system, i.e. the decimal digits.

<span class="mw-page-title-main">Positional notation</span> Method for representing or encoding numbers

Positional notation usually denotes the extension to any base of the Hindu–Arabic numeral system. More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred. In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string.

<span class="mw-page-title-main">Ancient Mesopotamian units of measurement</span>

Ancient Mesopotamian units of measurement originated in the loosely organized city-states of Early Dynastic Sumer. Each city, kingdom and trade guild had its own standards until the formation of the Akkadian Empire when Sargon of Akkad issued a common standard. This standard was improved by Naram-Sin, but fell into disuse after the Akkadian Empire dissolved. The standard of Naram-Sin was readopted in the Ur III period by the Nanše Hymn which reduced a plethora of multiple standards to a few agreed upon common groupings. Successors to Sumerian civilization including the Babylonians, Assyrians, and Persians continued to use these groupings. Akkado-Sumerian metrology has been reconstructed by applying statistical methods to compare Sumerian architecture, architectural plans, and issued official standards such as Statue B of Gudea and the bronze cubit of Nippur.

<span class="mw-page-title-main">Hindu–Arabic numeral system</span> Most common system for writing numbers

The Hindu–Arabic numeral system or Indo-Arabic numeral system is a positional base ten numeral system for representing integers; its extension to non-integers is the decimal numeral system, which is presently the most common numeral system.

<span class="mw-page-title-main">Babylonian mathematics</span> Mathematics in Mesopotamia 1830–539 BC

Babylonian mathematics is the mathematics developed or practiced by the people of Mesopotamia, from the days of the early Sumerians to the centuries following the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited. With respect to time they fall in two distinct groups: one from the Old Babylonian period, the other mainly Seleucid from the last three or four centuries BC. With respect to content, there is scarcely any difference between the two groups of texts. Babylonian mathematics remained constant, in character and content, for over a millennium.

Non-standard positional numeral systems here designates numeral systems that may loosely be described as positional systems, but that do not entirely comply with the following description of standard positional systems:

A sign-value notation represents numbers using a sequence of numerals which each represent a distinct quantity, regardless of their position in the sequence. Sign-value notations are typically additive, subtractive, or multiplicative depending on their conventions for grouping signs together to collectively represent numbers.

Number systems have progressed from the use of fingers and tally marks, perhaps more than 40,000 years ago, to the use of sets of glyphs able to represent any conceivable number efficiently. The earliest known unambiguous notations for numbers emerged in Mesopotamia about 5000 or 6000 years ago.

A timeline of numerals and arithmetic.

An alphabetic numeral system is a type of numeral system. Developed in classical antiquity, it flourished during the early Middle Ages. In alphabetic numeral systems, numbers are written using the characters of an alphabet, syllabary, or another writing system. Unlike acrophonic numeral systems, where a numeral is represented by the first letter of the lexical name of the numeral, alphabetic numeral systems can arbitrarily assign letters to numerical values. Some systems, including the Arabic, Georgian and Hebrew systems, use an already established alphabetical order. Alphabetic numeral systems originated with Greek numerals around 600 BC and became largely extinct by the 16th century. After the development of positional numeral systems like Hindu–Arabic numerals, the use of alphabetic numeral systems dwindled to predominantly ordered lists, pagination, religious functions, and divinatory magic.

References

  1. 1 2 3 Stephen Chrisomalis (2010). Numerical Notation: A Comparative History. Cambridge University Press. p. 247. ISBN   978-0-521-87818-0.
  2. 1 2 Stephen Chrisomalis (2010). Numerical Notation: A Comparative History. Cambridge University Press. p. 248. ISBN   978-0-521-87818-0.
  3. ↑ Scientific American – Why is a minute divided into 60 seconds, an hour into 60 minutes, yet there are only 24 hours in a day?
  4. ↑ Lamb, Evelyn (August 31, 2014), "Look, Ma, No Zero!", Scientific American , Roots of Unity

Bibliography

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.