
In thermodynamics, an adiabatic process is a type of thermodynamic process which occurs without transferring heat or mass between the system and its surroundings. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work. It also conceptually supports the theory used to explain the first law of thermodynamics and is therefore a key thermodynamic concept.

The Diesel cycle is a combustion process of a reciprocating internal combustion engine. In it, fuel is ignited by heat generated during the compression of air in the combustion chamber, into which fuel is then injected. This is in contrast to igniting the fuel-air mixture with a spark plug as in the Otto cycle (four-stroke/petrol) engine. Diesel engines are used in aircraft, automobiles, power generation, diesel-electric locomotives, and both surface ships and submarines.

In thermodynamics and engineering, a heat engine is a system that converts heat or thermal energy to mechanical energy, which can then be used to do mechanical work. It does this by bringing a working substance from a higher state temperature to a lower state temperature. A heat source generates thermal energy that brings the working substance to the high temperature state. The working substance generates work in the working body of the engine while transferring heat to the colder sink until it reaches a low temperature state. During this process some of the thermal energy is converted into work by exploiting the properties of the working substance. The working substance can be any system with a non-zero heat capacity, but it usually is a gas or liquid. During this process, some heat is normally lost to the surroundings and is not converted to work. Also, some energy is unusable because of friction and drag.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

An Otto cycle is an idealized thermodynamic cycle that describes the functioning of a typical spark ignition piston engine. It is the thermodynamic cycle most commonly found in automobile engines.

In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes.

In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature of the system remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and the change in the system will occur slowly enough to allow the system to continue to adjust to the temperature of the reservoir through heat exchange. In contrast, an adiabatic process is where a system exchanges no heat with its surroundings (Q = 0).

The Brayton cycle is a thermodynamic cycle named after George Brayton that describes the workings of a constant-pressure heat engine. The original Brayton engines used a piston compressor and piston expander, but more modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle. Although the cycle is usually run as an open system, it is conventionally assumed for the purposes of thermodynamic analysis that the exhaust gases are reused in the intake, enabling analysis as a closed system.

In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the system stays constant: ΔP = 0. The heat transferred to the system does work, but also changes the internal energy (U) of the system. This article uses the physics sign convention for work, where positive work is work done by the system. Using this convention, by the first law of thermodynamics,

A compressor is a mechanical device that increases the pressure of a gas by reducing its volume. An air compressor is a specific type of gas compressor.

The Rankine cycle is a model used to predict the performance of steam turbine systems. It was also used to study the performance of reciprocating steam engines. The Rankine cycle is an idealized thermodynamic cycle of a heat engine that converts heat into mechanical work while undergoing phase change. It is an idealized cycle in which friction losses in each of the four components are neglected. The heat is supplied externally to a closed loop, which usually uses water as the working fluid. It is named after William John Macquorn Rankine, a Scottish polymath and Glasgow University professor.

In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume. It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) for an ideal gas or κ (kappa), the isentropic exponent for a real gas. The symbol γ is used by aerospace and chemical engineers.
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
In fluid dynamics, stagnation pressure is the static pressure at a stagnation point in a fluid flow. At a stagnation point the fluid velocity is zero. In an incompressible flow, stagnation pressure is equal to the sum of the free-stream static pressure and the free-stream dynamic pressure.

A thermodynamic cycle consists of a linked sequence of thermodynamic processes that involve transfer of heat and work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state. In the process of passing through a cycle, the working fluid (system) may convert heat from a warm source into useful work, and dispose of the remaining heat to a cold sink, thereby acting as a heat engine. Conversely, the cycle may be reversed and use work to move heat from a cold source and transfer it to a warm sink thereby acting as a heat pump. At every point in the cycle, the system is in thermodynamic equilibrium, so the cycle is reversible.

In thermodynamics, the thermal efficiency is a dimensionless performance measure of a device that uses thermal energy, such as an internal combustion engine, a steam turbine or a steam engine, a boiler, furnace, or a refrigerator for example. For a heat engine, thermal efficiency is the fraction of the energy added by heat that is converted to net work output. In the case of a refrigeration or heat pump cycle, thermal efficiency is the ratio of net heat output for heating, or removal for cooling, to energy input.

A polytropic process is a thermodynamic process that obeys the relation:
In classical thermodynamics, entropy is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-nineteenth century from the Greek word τρoπή (transformation) to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy. The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.
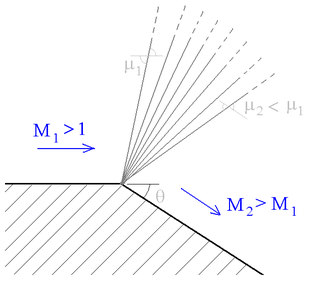
A supersonic expansion fan, technically known as Prandtl–Meyer expansion fan, a two-dimensional simple wave, is a centered expansion process that occurs when a supersonic flow turns around a convex corner. The fan consists of an infinite number of Mach waves, diverging from a sharp corner. When a flow turns around a smooth and circular corner, these waves can be extended backwards to meet at a point.
Fanno flow is the adiabatic flow through a constant area duct where the effect of friction is considered. Compressibility effects often come into consideration, although the Fanno flow model certainly also applies to incompressible flow. For this model, the duct area remains constant, the flow is assumed to be steady and one-dimensional, and no mass is added within the duct. The Fanno flow model is considered an irreversible process due to viscous effects. The viscous friction causes the flow properties to change along the duct. The frictional effect is modeled as a shear stress at the wall acting on the fluid with uniform properties over any cross section of the duct.









































