List of uniform polyhedra by vertex figure

Polyhedron
Class	Number and properties
Platonic solids	(5, convex, regular)
Archimedean solids	(13, convex, uniform)
Kepler–Poinsot polyhedra	(4, regular, non-convex)
Uniform polyhedra	(75, uniform)
Prismatoid: prisms, antiprisms etc.	(4 infinite uniform classes)
Polyhedra tilings	(11 regular, in the plane)
Quasi-regular polyhedra	(8)
Johnson solids	(92, convex, non-uniform)
Pyramids and Bipyramids	(infinite)
Stellations	Stellations
Polyhedral compounds	(5 regular)
Deltahedra	(Deltahedra, equilateral triangle faces)
Snub polyhedra	(12 uniform, not mirror image)
Zonohedron	(Zonohedra, faces have 180°symmetry)
Dual polyhedron
Self-dual polyhedron	(infinite)
Catalan solid	(13, Archimedean dual)

There are many relations among the uniform polyhedra. ^{[1] [2] [3]} Some are obtained by truncating the vertices of the regular or quasi-regular polyhedron. Others share the same vertices and edges as other polyhedron. The grouping below exhibit some of these relations.

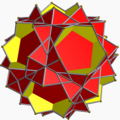
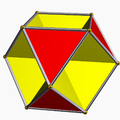
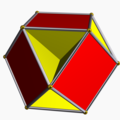
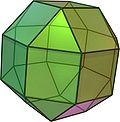
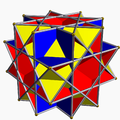
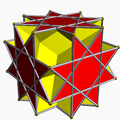
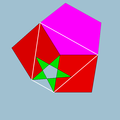
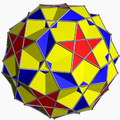
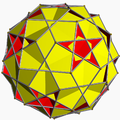
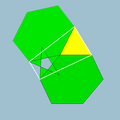
The vertex figure of a polyhedron

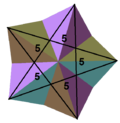
The relations can be made apparent by examining the vertex figures obtained by listing the faces adjacent to each vertex (remember that for uniform polyhedra all vertices are the same, that is vertex-transitive). For example, the cube has vertex figure 4.4.4, which is to say, three adjacent square faces. The possible faces are

• 3 - equilateral triangle
• 4 - square
• 5 - regular pentagon
• 6 - regular hexagon
• 8 - regular octagon
• 10 - regular decagon
• 5/2 - pentagram
• 8/3 - octagram
• 10/3 - decagram

Some faces will appear with reverse orientation which is written here as

• -3 - a triangle with reverse orientation (often written as 3/2)

Others pass through the origin which we write as

• 6* - hexagon passing through the origin

The Wythoff symbol relates the polyhedron to spherical triangles. Wythoff symbols are written p|q r, p q|r, p q r| where the spherical triangle has angles π/p,π/q,π/r, the bar indicates the position of the vertices in relation to the triangle.

Example vertex figures

Johnson (2000) classified uniform polyhedra according to the following:

1. Regular (regular polygonal vertex figures): p^q, Wythoff symbol q|p 2
2. Quasi-regular (rectangular or ditrigonal vertex figures): p.q.p.q 2|p q, or p.q.p.q.p.q, Wythoff symbol 3|p q
3. Versi-regular (orthodiagonal vertex figures), p.q*.-p.q*, Wythoff symbol q q|p
4. Truncated regular (isosceles triangular vertex figures): p.p.q, Wythoff symbol q 2|p
5. Versi-quasi-regular (dipteroidal vertex figures), p.q.p.r Wythoff symbol q r|p
6. Quasi-quasi-regular (trapezoidal vertex figures): p*.q.p*.-r q.r|p or p.q*.-p.q* p q r|
7. Truncated quasi-regular (scalene triangular vertex figures), p.q.r Wythoff symbol p q r|
8. Snub quasi-regular (pentagonal, hexagonal, or octagonal vertex figures), Wythoff symbol p q r|
9. Prisms (truncated hosohedra),
10. Antiprisms and crossed antiprisms (snub dihedra)

The format of each figure follows the same basic pattern

1. image of polyhedron
2. name of polyhedron
3. alternate names (in brackets)
4. Wythoff symbol
5. Numbering systems: W - number used by Wenninger in polyhedra models , U - uniform indexing, K - Kaleido indexing, C - numbering used in Coxeter et al. 'Uniform Polyhedra'.
6. Number of vertices V, edges E, Faces F and number of faces by type.
7. Euler characteristic χ = V - E + F

The vertex figures are on the left, followed by the Point groups in three dimensions#The seven remaining point groups, either tetrahedral T_d, octahedral O_h or icosahedral I_h.

Truncated forms

Regular polyhedra and their truncated forms

Column A lists all the regular polyhedra, column B list their truncated forms. Regular polyhedra all have vertex figures p^r: p.p.p etc. and Wythoff symbol p|q r. The truncated forms have vertex figure q.q.r (where q=2p and r) and Wythoff p q|r.

vertex figure	group	A: regular: p.p.p	B: truncated regular: p.p.r
3.3.3 3.6.6	Td	Tetrahedron 3|2 3 W1, U01, K06, C15 V 4,E 6,F 4=4{3} χ=2	Truncated tetrahedron 2 3|3 W6, U02, K07, C16 V 12,E 18,F 8=4{3}+4{6} χ=2
3.3.3.3 4.6.6	Oh	Octahedron 4|2 3, 34 W2, U05, K10, C17 V 6,E 12,F 8=8{3} χ=2	Truncated octahedron 2 4|3 W7, U08, K13, C20 V 24,E 36,F 14=6{4}+8{6} χ=2
4.4.4 3.8.8	Oh	Hexahedron (Cube) 3|2 4 W3, U06, K11, C18 V 8,E 12,F 6=6{4} χ=2	Truncated hexahedron 2 3|4 W8, U09, K14, C21 V 24,E 36,F 14=8{3}+6{8} χ=2
3.3.3.3.3 5.6.6	Ih	Icosahedron 5|2 3 W4, U22, K27, C25 V 12,E 30,F 20=20{3} χ=2	Truncated icosahedron 2 5|3 W9, U25, K30, C27 E 60,V 90,F 32=12{5}+20{6} χ=2
5.5.5 3.10.10	Ih	Dodecahedron 3|2 5 W5, U23, K28, C26 V 20,E 30,F 12=12{5} χ=2	Truncated dodecahedron 2 3|5 W10, U26, K31, C29 V 60,E 90,F 32=20{3}+12{10} χ=2
5.5.5.5.5 5/2.10.10	Ih	Great dodecahedron 5/2|2 5 W21, U35, K40, C44 V 12,E 30,F 12=12{5} χ=-6	Truncated great dodecahedron 25/2|5 W75, U37, K42, C47 V 60,E 90,F 24=12{5/2}+12{10} χ=-6
3.3.3.3.3 5/2.6.6.	Ih	Great icosahedron (16th stellation of icosahedron) 5/2|2 3 W41, U53, K58, C69 V 12,E 30,F 20=20{3} χ=2	Great truncated icosahedron 25/2|3 W95, U55, K60, C71 V 60,E 90,F 32=12{5/2}+20{6} χ=2
5/2.5/2.5/2.5/2.5/2	Ih	Small stellated dodecahedron 5|25/2 W20, U34, K39, C43 V 12,E 30,F 12=12{5/2} χ=-6
5/2.5/2.5/2	Ih	Great stellated dodecahedron 3|25/2 W22, U52, K57, C68 V 20,E 30,F 12=12{5/2} χ=2

In addition there are three quasi-truncated forms. These also class as truncated-regular polyhedra.

vertex figures	Group Oh	Group Ih	Group Ih
3.8/3.8/3 5.10/3.10/3 3.10/3.10/3	Stellated truncated hexahedron (Quasitruncated hexahedron) (stellatruncated cube) 2 3|4/3 W92, U19, K24, C66 V 24,E 36,F 14=8{3}+6{8/3} χ=2	Small stellated truncated dodecahedron (Quasitruncated small stellated dodecahedron) (Small stellatruncated dodecahedron) 2 5|5/3 W97, U58, K63 V 60,E 90,F 24=12{5}+12{10/3} χ=-6	Great stellated truncated dodecahedron (Quasitruncated great stellated dodecahedron) (Great stellatruncated dodecahedron) 2 3|5/3 W104, U66, K71, C83 V 60,E 90,F 32=20{3}+12{10/3} χ=2

Truncated forms of quasi-regular polyhedra

Column A lists some quasi-regular polyhedra, column B lists normal truncated forms, column C shows quasi-truncated forms, column D shows a different method of truncation. These truncated forms all have a vertex figure p.q.r and a Wythoff symbol p q r|.

vertex figure	group	A: quasi-regular: p.q.p.q	B: truncated quasi-regular: p.q.r	C: truncated quasi-regular: p.q.r	D: truncated quasi-regular: p.q.r
3.4.3.4 4.6.8 4.6.8/3 8.6.8/3	Oh	Cuboctahedron 2|3 4 W11, U07, K12, C19 V 12,E 24,F 14=8{3}+6{4} χ=2	Truncated cuboctahedron (Great rhombicuboctahedron) 2 3 4| W15, U11, K16, C23 V 48,E 72,F 26=12{4}+8{6}+6{8} χ=2	Great truncated cuboctahedron (Quasitruncated cuboctahedron) 2 34/3| W93, U20, K25, C67 V 48,E 72,F 26=12{4}+8{6}+6{8/3} χ=2	Cubitruncated cuboctahedron (Cuboctatruncated cuboctahedron) 3 44/3| W79, U16, K21, C52 V 48,E 72,F 20=8{6}+6{8}+6{8/3} χ=-4
3.5.3.5 4.6.10 4.6.10/3 10.6.10/3	Ih	Icosidodecahedron 2|3 5 W12, U24, K29, C28 V 30,E 60,F 32=20{3}+12{5} χ=2	Truncated icosidodecahedron (Great rhombicosidodecahedron) 2 3 5| W16, U28, K33, C31 V 120,E 180,F 62=30{4}+20{6}+12{10} χ=2	Great truncated icosidodecahedron (Great quasitruncated icosidodecahedron) 2 35/3| W108, U68, K73, C87 V 120,E 180,F 62=30{4}+20{6}+12{10/3} χ=2	Icositruncated dodecadodecahedron (Icosidodecatruncated icosidodecahedron) 3 55/3| W84, U45, K50, C57 V 120,E 180,F 44=20{6}+12{10}+12{10/3} χ=-16
5/2.5.5/2.5 4.10.10/3	Ih	Dodecadodecahedron 2 5|5/2 W73, U36, K41, C45 V 30,E 60, F 24=12{5}+12{5/2} χ=-6		Truncated dodecadodecahedron (Quasitruncated dodecahedron) 2 55/3| W98, U59, K64, C75 V 120,E 180,F 54=30{4}+12{10}+12{10/3} χ=-6
3.5/2.3.5/2	Ih	Great icosidodecahedron 2 3|5/2 W94, U54, K59, C70 V 30,E 60, F 32=20{3}+12{5/2} χ=2

Polyhedra sharing edges and vertices

Regular

These are all mentioned elsewhere, but this table shows some relations. They are all regular apart from the tetrahemihexahedron which is versi-regular.

vertex figure	V	E	group	regular	regular/versi-regular
3.3.3.3 3.4*.-3.4*	6	12	Oh	Octahedron 4|2 3 W2, U05, K10, C17 F 8=8{3} χ=2	Tetrahemihexahedron 3/23|2 W67, U04, K09, C36 F 7=4{3}+3{4} χ=1
3.3.3.3.3 5.5.5.5.5	12	30	Ih	Icosahedron 5|2 3 W4, U22, K27 F 20=20{3} χ=2	Great dodecahedron 5/2|2 5 W21, U35, K40, C44 F 12=12{5} χ=-6
5/2.5/2.5/2.5/2.5/2 3.3.3.3.3	12	30	Ih	Small stellated dodecahedron 5|25/2 W20, U34, K39, C43 F 12=12{5/2} χ=-6	Great icosahedron (16th stellation of icosahedron) 5/2|2 3 W41, U53, K58, C69 F 20=20{3} χ=2

Quasi-regular and versi-regular

Rectangular vertex figures, or crossed rectangles first column are quasi-regular second and third columns are hemihedra with faces passing through the origin, called versi-regular by some authors.

vertex figure	V	E	group	quasi-regular: p.q.p.q	versi-regular: p.s*.-p.s*	versi-regular: q.s*.-q.s*
3.4.3.4 3.6*.-3.6* 4.6*.-4.6*	12	24	Oh	Cuboctahedron 2|3 4 W11, U07, K12, C19 F 14=8{3}+6{4} χ=2	Octahemioctahedron 3/23|3 W68, U03, K08, C37 F 12=8{3}+4{6} χ=0	Cubohemioctahedron 4/34|3 W78, U15, K20, C51 F 10=6{4}+4{6} χ=-2
3.5.3.5 3.10*.-3.10* 5.10*.-5.10*	30	60	Ih	Icosidodecahedron 2|3 5 W12, U24, K29, C28 F 32=20{3}+12{5} χ=2	Small icosihemidodecahedron 3/23|5 W89, U49, K54, C63 F 26=20{3}+6{10} χ=-4	Small dodecahemidodecahedron 5/45|5 W91, U51, K56, 65 F 18=12{5}+6{10} χ=-12
3.5/2.3.5/2 3.10*.-3.10* 5/2.10*.-5/2.10*	30	60	Ih	Great icosidodecahedron 2|5/23 W94, U54, K59, C70 F 32=20{3}+12{5/2} χ=2	Great icosihemidodecahedron 3 3|5/3 W106, U71, K76, C85 F 26=20{3}+6{10/3} χ=-4	Great dodecahemidodecahedron 5/35/2|5/3 W107, U70, K75, C86 F 18=12{5/2}+6{10/3} χ=-12
5.5/2.5.5/2 5.6*.-5.6* 5/2.6*.-5/2.6*	30	60	Ih	Dodecadodecahedron 2|5/25 W73, U36, K41, C45 F 24=12{5}+12{5/2} χ=-6	Great dodecahemicosahedron 5/45|3 W102, U65, K70, C81 F 22=12{5}+10{6} χ=-8	Small dodecahemicosahedron 5/35/2|3 W100, U62, K67, C78 F 22=12{5/2}+10{6} χ=-8

Ditrigonal regular and versi-regular

Ditrigonal (that is di(2) -tri(3)-ogonal) vertex figures are the 3-fold analog of a rectangle. These are all quasi-regular as all edges are isomorphic. The compound of 5-cubes shares the same set of edges and vertices. The cross forms have a non-orientable vertex figure so the "-" notation has not been used and the "*" faces pass near rather than through the origin.

vertex figure	V	E	group	ditrigonal	crossed-ditrigonal	crossed-ditrigonal
5/2.3.5/2.3.5/2.3 5/2.5*.5/2.5*.5/2.5* 3.5*.3.5*.3.5*	20	60	Ih	Small ditrigonal icosidodecahedron 3|5/23 W70, U30, K35, C39 F 32=20{3}+12{5/2} χ=-8	Ditrigonal dodecadodecahedron 3|5/35 W80, U41, K46, C53 F 24=12{5}+12{5/2} χ=-16	Great ditrigonal icosidodecahedron 3/2|3 5 W87, U47, K52, C61 F 32=20{3}+12{5} χ=-8

versi-quasi-regular and quasi-quasi-regular

Group III: trapezoid or crossed trapezoid vertex figures. The first column include the convex rhombic polyhedra, created by inserting two squares into the vertex figures of the Cuboctahedron and Icosidodecahedron.

vertex figure	V	E	group	trapezoid: p.q.r.q	crossed-trapezoid: p.s*.-r.s*	crossed-trapezoid: q.s*.-q.s*
3.4.4.4 3.8*.-4.8* 4.8*.-4.8*	24	48	Oh	Small rhombicuboctahedron (rhombicuboctahedron) 3 4|2 W13, U10, K15, C22 F 26=8{3}+(6+12){4} χ=2	Small cubicuboctahedron 3/24|4 W69, U13, K18, C38 F 20=8{3}+6{4}+6{8} χ=-4	Small rhombihexahedron 2 3/2 4| W86, U18, K23, C60 F 18=12{4}+6{8} χ=-6
3.8/3.4.8/3 3.4*.-4.4* 8/3.4*.-8/3.4*	24	48	Oh	Great cubicuboctahedron 3 4|4/3 W77, U14, K19, C50 F 20=8{3}+6{4}+6{8/3} χ=-4	Nonconvex great rhombicuboctahedron (Quasirhombicuboctahedron) 3/24|2 W85, U17, K22, C59 F 26=8{3}+(6+12){4} χ=2	Great rhombihexahedron 2 4/33/2| W103, U21, K26, C82 F 18=12{4}+6{8/3} χ=-6
3.4.5.4 3.10*.-5.10* 4.10*.-4.10*	60	120	Ih	Small rhombicosidodecahedron (rhombicosidodecahedron) 3 5|2 W14, U27, K32, C30 F 62=20{3}+30{4}+12{5} χ=2	Small dodecicosidodecahedron 3/25|5 W72, U33, K38, C42 F 44=20{3}+12{5}+12{10} χ=-16	Small rhombidodecahedron 25/25| W74, U39, K44, C46 F 42=30{4}+12{10} χ=-18
5/2.4.5.4 5/2.6*.-5.6* 4.6*.-4.6*	60	120	Ih	Rhombidodecadodecahedron 5/25|2 W76, U38, K43, C48 F 54=30{4}+12{5}+12{5/2} χ=-6	Icosidodecadodecahedron 5/35|3 W83, U44, K49, C56 F 44=12{5}+12{5/2}+20{6} χ=-16	Rhombicosahedron 2 35/2| W96, U56, K61, C72 F 50=30{4}+20{6} χ=-10
3.10/3.5/2.10/3 3.4*.-5/2.4* 10/3.4*.-10/3.4*	60	120	Ih	Great dodecicosidodecahedron 5/23|5/3 W99, U61, K66, C77 F 44=20{3}+12{5/2}+12{10/3 } χ=-16	Nonconvex great rhombicosidodecahedron (Quasirhombicosidodecahedron) 5/33|2 W105, U67, K72, C84 F 62=20{3}+30{4}+12{5/2} χ=2	Great rhombidodecahedron 2 3/25/3| W109, U73, K78, C89 F 42=30{4}+12{10/3} χ=-18
3.6.5/2.6 3.10*.-5/2.10* 6.10*.-6.10*	60	120	Ih	Small icosicosidodecahedron 5/23|3 W71, U31, K36, C40 F 52=20{3}+12{5/2}+20{6} χ=-8	Small ditrigonal dodecicosidodecahedron 5/33|5 W82, U43, K48, C55 F 44=20{3}+12{5/2}+12{10} χ=-16	Small dodecicosahedron 3 3/2 5| W90, U50, K55, C64 F 32=20{6}+12{10} χ=-28
3.10/3.5.10/3 3.6*.-5.6* 10/3.6*.-10/3.6*	60	120	Ih	Great ditrigonal dodecicosidodecahedron 3 5|5/3 W81, U42, K47, C54 F 44=20{3}+12{5}+12{10/3} χ=-16	Great icosicosidodecahedron 3/25|3 W88, U48, K53, C62 F 52=20{3}+12{5}+20{6} χ=-8	Great dodecicosahedron 3 5/35/2| W101, U63, K68, C79 F 32=20{6}+12{10/3} χ=-28

References

1. Coxeter, H. S. M.; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London, 246: 401–450 (6 plates), doi:10.1098/rsta.1954.0003, MR   0062446 .
2. Sopov, S. P. (1970), "A proof of the completeness on the list of elementary homogeneous polyhedra", Ukrainskiĭ Geometricheskiĭ Sbornik (8): 139–156, MR   0326550 .
3. Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London, 278: 111–135, doi:10.1098/rsta.1975.0022, MR   0365333 .