In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.
In mathematics, a measurable cardinal is a certain kind of large cardinal number. In order to define the concept, one introduces a two-valued measure on a cardinal κ, or more generally on any set. For a cardinal κ, it can be described as a subdivision of all of its subsets into large and small sets such that κ itself is large, ∅ and all singletons {α}, α ∈ κ are small, complements of small sets are large and vice versa. The intersection of fewer than κ large sets is again large.

In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph.
Zermelo set theory, as set out in a seminal paper in 1908 by Ernst Zermelo, is the ancestor of modern Zermelo–Fraenkel set theory (ZF) and its extensions, such as von Neumann–Bernays–Gödel set theory (NBG). It bears certain differences from its descendants, which are not always understood, and are frequently misquoted. This article sets out the original axioms, with the original text and original numbering.
In mathematics, in set theory, the constructible universe, denoted by , is a particular class of sets that can be described entirely in terms of simpler sets. is the union of the constructible hierarchy. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this paper, he proved that the constructible universe is an inner model of ZF set theory, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axioms of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
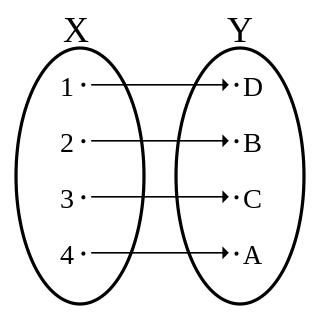
In mathematics, two sets or classes A and B are equinumerous if there exists a one-to-one correspondence (or bijection) between them, that is, if there exists a function from A to B such that for every element y of B, there is exactly one element x of A with f(x) = y. Equinumerous sets are said to have the same cardinality (number of elements). The study of cardinality is often called equinumerosity (equalness-of-number). The terms equipollence (equalness-of-strength) and equipotence (equalness-of-power) are sometimes used instead.
The von Neumann cardinal assignment is a cardinal assignment that uses ordinal numbers. For a well-orderable set U, we define its cardinal number to be the smallest ordinal number equinumerous to U, using the von Neumann definition of an ordinal number. More precisely:
In mathematics, particularly in set theory, the beth numbers are a certain sequence of infinite cardinal numbers, conventionally written , where is the second Hebrew letter (beth). The beth numbers are related to the aleph numbers, but unless the generalized continuum hypothesis is true, there are numbers indexed by that are not indexed by .
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by V, is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930.
In mathematical logic, New Foundations (NF) is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name. Much of this entry discusses NF with urelements (NFU), an important variant of NF due to Jensen and clarified by Holmes. In 1940 and in a revision in 1951, Quine introduced an extension of NF sometimes called "Mathematical Logic" or "ML", that included proper classes as well as sets.
In set theory, the cardinality of the continuum is the cardinality or "size" of the set of real numbers , sometimes called the continuum. It is an infinite cardinal number and is denoted by or .
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set that represents the result of the operation or by using transfinite recursion. Cantor normal form provides a standardized way of writing ordinals. In addition to these usual ordinal operations, there are also the "natural" arithmetic of ordinals and the nimber operations.
In mathematical logic, the theory of infinite sets was first developed by Georg Cantor. Although this work has become a thoroughly standard fixture of classical set theory, it has been criticized in several areas by mathematicians and philosophers.
In mathematics, specifically in axiomatic set theory, a Hartogs number is an ordinal number associated with a set. In particular, if X is any set, then the Hartogs number of X is the least ordinal α such that there is no injection from α into X. If X can be well-ordered then the cardinal number of α is a minimal cardinal greater than that of X. If X cannot be well-ordered then there cannot be an injection from X to α. However, the cardinal number of α is still a minimal cardinal not less than or equal to the cardinality of X. The map taking X to α is sometimes called Hartogs's function. This mapping is used to construct the aleph numbers, which are all the cardinal numbers of infinite well-orderable sets.
This article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC and in NFU, the version of Quine's New Foundations shown to be consistent by R. B. Jensen in 1969.

In set theory, the axiom of limitation of size was proposed by John von Neumann in his 1925 axiom system for sets and classes. It formalizes the limitation of size principle, which avoids the paradoxes encountered in earlier formulations of set theory by recognizing that some classes are too big to be sets. Von Neumann realized that the paradoxes are caused by permitting these big classes to be members of a class. A class that is a member of a class is a set; a class that is not a set is a proper class. Every class is a subclass of V, the class of all sets. The axiom of limitation of size says that a class is a set if and only if it is smaller than V—that is, there is no function mapping it onto V. Usually, this axiom is stated in the equivalent form: A class is a proper class if and only if there is a function that maps it onto V.
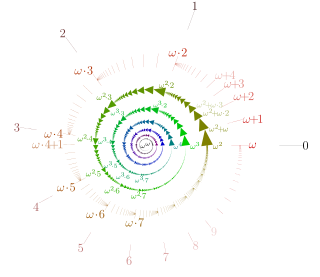
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
This is a glossary of set theory.









