Elongated cupola

Set of elongated cupolae
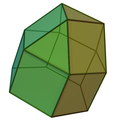
Elongated pentagonal cupola
Faces	n triangles 3n squares 1 n-gon 1 2n-gon
Edges	9n
Vertices	5n
Symmetry group	Cnv, [n], (*nn)
Rotational group	Cn, [n]+, (nn)
Dual polyhedron
Properties	convex

In geometry, the elongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to a 2n-gonal prism.

There are three elongated cupolae that are Johnson solids made from regular triangles, squares, and pentagons. Higher forms can be constructed with isosceles triangles. Adjoining a triangular prism to a cube also generates a polyhedron, but has two pairs of coplanar faces, so is not a Johnson solid. Higher forms can be constructed without regular faces.

Forms

	name	faces
	elongated digonal cupola	2 triangles, 6+1 squares
	elongated triangular cupola (J18)	3+1 triangles, 9 squares, 1 hexagon
	elongated square cupola (J19)	4 triangles, 12+1 squares, 1 octagon
	elongated pentagonal cupola (J20)	5 triangles, 15 squares, 1 pentagon, 1 decagon
	elongated hexagonal cupola	6 triangles, 18 squares, 1 hexagon, 1 dodecagon

See also

• Gyroelongated cupola
• Bicupola
• Elongated bicupola
• Gyroelongated bicupola
• Rotunda

References

• Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.