Bicupola

In geometry, a bicupola is a solid formed by connecting two cupolae on their bases. Here, two classes of bicupola are included because each cupola (bicupola half) is bordered by alternating triangles and squares. If similar faces are attached together the result is an orthobicupola; if squares are attached to triangles it is a gyrobicupola.

Forms

In the first column of the two following tables, the symbols are Schoenflies, Coxeter, and orbifold notation, in this order.

Set of orthobicupolae

Symmetry	Picture	Description
D3h [2,3] *223		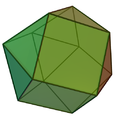Triangular orthobicupola (J27): 8 triangles, 6 squares. [1] [2] Its dual is the trapezo-rhombic dodecahedron
D4h [2,4] *224		Square orthobicupola (J28): 8 triangles, 10 squares. [2]
D5h [2,5] *225		Pentagonal orthobicupola (J30): 10 triangles, 10 squares, 2 pentagons. [2]
Dnh [2,n] *22n		n-gonal orthobicupola: 2n triangles, 2n rectangles, 2 n-gons

Set of gyrobicupolae

An n-gonal gyrobicupola has the same topology as an n-gonal rectified antiprism, Conway polyhedron notation: aAn.^{[ clarification needed ]}

Symmetry	Picture	Description
D2d [2+,4] 2*2		Gyrobifastigium (J26) or digonal gyrobicupola: 4 triangles, 4 squares.[ citation needed ]
D3d [2+,6] 2*3		Triangular gyrobicupola or cuboctahedron: 8 triangles, 6 squares. [1] [2] Its dual is the rhombic dodecahedron.
D4d [2+,8] 2*4		Square gyrobicupola (J29): 8 triangles, 10 squares. [2] Its dual is the elongated tetragonal trapezohedron
D5d [2+,10] 2*5		Pentagonal gyrobicupola (J31): 10 triangles, 10 squares, 2 pentagons. [2] Its dual is the elongated pentagonal trapezohedron
Dnd [2+,2n] 2*n		n-gonal gyrobicupola: 2n triangles, 2n rectangles, 2 n-gons.

See also

• Elongated cupola
• Gyroelongated cupola
• Elongated bicupola
• Gyroelongated bicupola
• Rotunda

References

1. Ogievetsky, O.; Shlosman, S. (2021). "Platonic compounds and cylinders". In Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry. American Mathematical Society. p. 477. ISBN   978-1-4704-5592-7.
2. Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR   0290245.