List of equations in fluid mechanics

This article summarizes equations in the theory of fluid mechanics.

Definitions

Flux F through a surface, dS is the differential vector area element, n is the unit normal to the surface. Left: No flux passes in the surface, the maximum amount flows normal to the surface. Right: The reduction in flux passing through a surface can be visualized by reduction in F or dS equivalently (resolved into components, θ is angle to normal n). F•dS is the component of flux passing through the surface, multiplied by the area of the surface (see dot product). For this reason flux represents physically a flow per unit area.

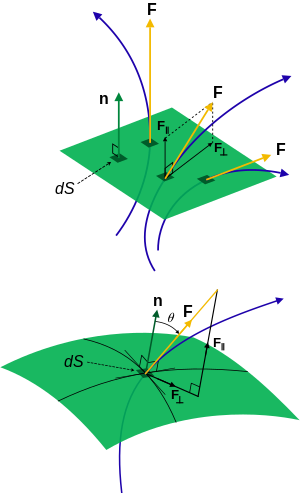
Here ${\displaystyle \mathbf {\hat {t}} \,\!}$ is a unit vector in the direction of the flow/current/flux.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Flow velocity vector field	u	${\displaystyle \mathbf {u} =\mathbf {u} \left(\mathbf {r} ,t\right)\,\!}$	m s−1	[L][T]−1
Velocity pseudovector field	ω	${\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {v} }$	s−1	[T]−1
Volume velocity, volume flux	φV (no standard symbol)	${\displaystyle \phi _{V}=\int _{S}\mathbf {u} \cdot \mathrm {d} \mathbf {A} \,\!}$	m3 s−1	[L]3 [T]−1
Mass current per unit volume	s (no standard symbol)	${\displaystyle s=\mathrm {d} \rho /\mathrm {d} t\,\!}$	kg m−3 s−1	[M] [L]−3 [T]−1
Mass current, mass flow rate	Im	${\displaystyle I_{\mathrm {m} }=\mathrm {d} m/\mathrm {d} t\,\!}$	kg s−1	[M][T]−1
Mass current density	jm	${\displaystyle I_{\mathrm {m} }=\iint \mathbf {j} _{\mathrm {m} }\cdot \mathrm {d} \mathbf {S} \,\!}$	kg m−2 s−1	[M][L]−2[T]−1
Momentum current	Ip	${\displaystyle I_{\mathrm {p} }=\mathrm {d} \left|\mathbf {p} \right|/\mathrm {d} t\,\!}$	kg m s−2	[M][L][T]−2
Momentum current density	jp	${\displaystyle I_{\mathrm {p} }=\iint \mathbf {j} _{\mathrm {p} }\cdot \mathrm {d} \mathbf {S} }$	kg m s−2	[M][L][T]−2

Equations

Physical situation	Nomenclature	Equations
Fluid statics, pressure gradient	r = Position ρ = ρ(r) = Fluid density at gravitational equipotential containing r g = g(r) = Gravitational field strength at point r ∇P = Pressure gradient	${\displaystyle \nabla P=\rho \mathbf {g} \,\!}$
Buoyancy equations	ρf = Mass density of the fluid Vimm = Immersed volume of body in fluid Fb = Buoyant force Fg = Gravitational force Wapp = Apparent weight of immersed body W = Actual weight of immersed body	Buoyant force ${\displaystyle \mathbf {F} _{\mathrm {b} }=-\rho _{f}V_{\mathrm {imm} }\mathbf {g} =-\mathbf {F} _{\mathrm {g} }\,\!}$ Apparent weight ${\displaystyle \mathbf {W} _{\mathrm {app} }=\mathbf {W} -\mathbf {F} _{\mathrm {b} }\,\!}$
Bernoulli's equation	pconstant is the total pressure at a point on a streamline	${\displaystyle p+\rho u^{2}/2+\rho gy=p_{\mathrm {constant} }\,\!}$
Euler equations	ρ = fluid mass density u is the flow velocity vector E = total volume energy density U = internal energy per unit mass of fluid p = pressure ${\displaystyle \otimes }$ denotes the tensor product	${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0\,\!}$ ${\displaystyle {\frac {\partial \rho {\mathbf {u} }}{\partial t}}+\nabla \cdot \left(\mathbf {u} \otimes \left(\rho \mathbf {u} \right)\right)+\nabla p=0\,\!}$ ${\displaystyle {\frac {\partial E}{\partial t}}+\nabla \cdot \left(\mathbf {u} \left(E+p\right)\right)=0\,\!}$ ${\displaystyle E=\rho \left(U+{\frac {1}{2}}\mathbf {u} ^{2}\right)\,\!}$
Convective acceleration		${\displaystyle \mathbf {a} =\left(\mathbf {u} \cdot \nabla \right)\mathbf {u} }$
Navier–Stokes equations	TD = Deviatoric stress tensor ${\displaystyle \mathbf {f} }$ = volume density of the body forces acting on the fluid ${\displaystyle \nabla }$ here is the del operator.	${\displaystyle \rho \left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} \right)=-\nabla p+\nabla \cdot \mathbf {T} _{\mathrm {D} }+\mathbf {f} }$

See also

• Defining equation (physical chemistry)
• List of electromagnetism equations
• List of equations in classical mechanics
• List of equations in gravitation
• List of equations in nuclear and particle physics
• List of equations in quantum mechanics
• List of photonics equations
• List of relativistic equations
• Table of thermodynamic equations

Sources

• P.M. Whelan, M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN   0-7195-3382-1.
• G. Woan (2010). The Cambridge Handbook of Physics Formulas . Cambridge University Press. ISBN   978-0-521-57507-2.
• A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN   978-0-07-025734-4.
• R.G. Lerner, G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN   978-0-07-025734-4.
• C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN   0-07-051400-3.
• P.A. Tipler, G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN   978-1-4292-0265-7.
• L.N. Hand, J.D. Finch (2008). Analytical Mechanics. Cambridge University Press. ISBN   978-0-521-57572-0.
• T.B. Arkill, C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray. ISBN   0-7195-2882-8.
• H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN   0-471-90182-2.

Further reading

• L.H. Greenberg (1978). Physics with Modern Applications . Holt-Saunders International W.B. Saunders and Co. ISBN   0-7216-4247-0.
• J.B. Marion, W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN   4-8337-0195-2.
• A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN   0-07-100144-1.
• H.D. Young, R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). ISBN   978-0-321-50130-1.