Natural numbers object

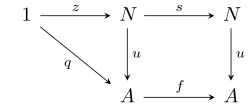
In category theory, a natural numbers object (NNO) is an object endowed with a recursive structure similar to natural numbers. More precisely, in a category E with a terminal object 1, an NNO N is given by:

1. a global element z : 1 → N, and
2. an arrow s : N → N,

such that for any object A of E, global element q : 1 → A, and arrow f : A → A, there exists a unique arrow u : N → A such that:

1. u ∘ z = q, and
2. u ∘ s = f ∘ u. ^{[1] [2] [3]}

In other words, the triangle and square in the following diagram commute.

The pair (q, f) is sometimes called the recursion data for u, given in the form of a recursive definition:

1. ⊢ u (z) = q
2. y ∈_EN ⊢ u (sy) = f (u (y))

The above definition is the universal property of NNOs, meaning they are defined up to canonical isomorphism. If the arrow u as defined above merely has to exist, that is, uniqueness is not required, then N is called a weak NNO.

Equivalent definitions

NNOs in cartesian closed categories (CCCs) or topoi are sometimes defined in the following equivalent way (due to Lawvere): for every pair of arrows g : A → B and f : B → B, there is a unique h : N × A → B such that the squares in the following diagram commute. ^[4]

This same construction defines weak NNOs in cartesian categories that are not cartesian closed.

In a category with a terminal object 1 and binary coproducts (denoted by +), an NNO can be defined as the initial algebra of the endofunctor that acts on objects by X ↦ 1 + X and on arrows by f ↦ id₁ + f. ^[5]

Properties

• Every NNO is an initial object of the category of diagrams of the form

${\displaystyle 1{\xrightarrow {~\quad q\quad ~}}A{\xrightarrow {~\quad f\quad ~}}A}$

• If a cartesian closed category has weak NNOs, then every slice of it also has a weak NNO.
• NNOs can be used for non-standard models of type theory in a way analogous to non-standard models of analysis. Such categories (or topoi) tend to have "infinitely many" non-standard natural numbers.^{[ clarification needed ]} (Like always, there are simple ways to get non-standard NNOs; for example, if z = s z, in which case the category or topos E is trivial.)
• Freyd showed that z and s form a coproduct diagram for NNOs; also, !_N : N → 1 is a coequalizer of s and 1_N, i.e., every pair of global elements of N are connected by means of s; furthermore, this pair of facts characterize all NNOs.

Examples

• In Set, the category of sets, the standard natural numbers are an NNO. ^[6] A terminal object in Set is a singleton, and a function out of a singleton picks out a single element of a set. The natural numbers 𝐍 are an NNO where z is a function from a singleton to 𝐍 whose image is zero, and s is the successor function. (We could actually allow z to pick out any element of 𝐍, and the resulting NNO would be isomorphic to this one.) One can prove that the diagram in the definition commutes using mathematical induction.
• In the category of types of Martin-Löf type theory (with types as objects and functions as arrows), the standard natural numbers type nat is an NNO. One can use the recursor for nat to show that the appropriate diagram commutes.
• Assume that ${\displaystyle {\mathcal {E}}}$ is a Grothendieck topos with terminal object ${\displaystyle \top }$ and that ${\displaystyle {\mathcal {E}}\simeq \mathbf {Shv} ({\mathfrak {C}},J)}$ for some Grothendieck topology ${\displaystyle J}$ on the category ${\displaystyle {\mathfrak {C}}}$. Then if ${\displaystyle \Gamma _{\mathbb {N} }}$ is the constant presheaf on ${\displaystyle {\mathfrak {C}}}$, then the NNO in ${\displaystyle {\mathcal {E}}}$ is the sheafification of ${\displaystyle \Gamma _{\mathbb {N} }}$ and may be shown to take the form $${\displaystyle \mathbb {N} _{\mathcal {E}}\cong \left(\Gamma _{\mathbb {N} }\right)^{++}\cong \coprod _{n\in \mathbb {N} }\top .}$$

See also

• Peano's axioms of arithmetic
• Categorical logic

References

1. Johnstone 2002, A2.5.1.
2. Lawvere 2005, p. 14.
3. Leinster, Tom (2014). "Rethinking set theory". American Mathematical Monthly. 121 (5): 403–415. arXiv: 1212.6543 . Bibcode:2012arXiv1212.6543L. doi:10.4169/amer.math.monthly.121.05.403. S2CID   5732995.
4. Johnstone 2002, A2.5.2.
5. Barr, Michael; Wells, Charles (1990). Category theory for computing science. New York: Prentice Hall. p. 358. ISBN   0131204866. OCLC   19126000.
6. Johnstone 2002, p. 108.

• Johnstone, Peter T. (2002). Sketches of an Elephant: a Topos Theory Compendium. Oxford: Oxford University Press. ISBN   0198534256. OCLC   50164783.
• Lawvere, William (2005) [1964]. "An elementary theory of the category of sets (long version) with commentary". Reprints in Theory and Applications of Categories. 11: 1–35.

External links

• Lecture notes from Robert Harper which discuss NNOs in Section 2.2: https://www.cs.cmu.edu/~rwh/courses/hott/notes/notes_week3.pdf
• A blog post by Clive Newstead on the n-Category Cafe: https://golem.ph.utexas.edu/category/2014/01/an_elementary_theory_of_the_ca.html
• Notes on datatypes as algebras for endofunctors by computer scientist Philip Wadler: http://homepages.inf.ed.ac.uk/wadler/papers/free-rectypes/free-rectypes.txt
• Notes on the nLab: https://ncatlab.org/nlab/show/ETCS