Wilks's lambda distribution

Last updated January 15, 2024

In statistics, Wilks' lambda distribution (named for Samuel S. Wilks), is a probability distribution used in multivariate hypothesis testing, especially with regard to the likelihood-ratio test and multivariate analysis of variance (MANOVA).

Definition

Wilks' lambda distribution is defined from two independent Wishart distributed variables as the ratio distribution of their determinants,^[1]

given

\mathbf {A} \sim W_{p}(\Sigma ,m)\qquad \mathbf {B} \sim W_{p}(\Sigma ,n)

independent and with $m\geq p$

\lambda ={\frac {\det(\mathbf {A} )}{\det(\mathbf {A+B} )}}={\frac {1}{\det(\mathbf {I} +\mathbf {A} ^{-1}\mathbf {B} )}}\sim \Lambda (p,m,n)

where p is the number of dimensions. In the context of likelihood-ratio tests m is typically the error degrees of freedom, and n is the hypothesis degrees of freedom, so that $n+m$ is the total degrees of freedom.^[1]

Approximations

Computations or tables of the Wilks' distribution for higher dimensions are not readily available and one usually resorts to approximations. One approximation is attributed to M. S. Bartlett and works for large m^[2] allows Wilks' lambda to be approximated with a chi-squared distribution

\left({\frac {p-n+1}{2}}-m\right)\log \Lambda (p,m,n)\sim \chi _{np}^{2}.

^[1]

Another approximation is attributed to C. R. Rao.^[1]^[3]

Properties

There is a symmetry among the parameters of the Wilks distribution,^[1]

\Lambda (p,m,n)\sim \Lambda (n,m+n-p,p)

Related distributions

The distribution can be related to a product of independent beta-distributed random variables

u_{i}\sim B\left({\frac {m+i-p}{2}},{\frac {p}{2}}\right)

\prod _{i=1}^{n}u_{i}\sim \Lambda (p,m,n).

As such it can be regarded as a multivariate generalization of the beta distribution.

It follows directly that for a one-dimension problem, when the Wishart distributions are one-dimensional with $p=1$ (i.e., chi-squared-distributed), then the Wilks' distribution equals the beta-distribution with a certain parameter set,

\Lambda (1,m,n)\sim B\left({\frac {m}{2}},{\frac {n}{2}}\right).

From the relations between a beta and an F-distribution, Wilks' lambda can be related to the F-distribution when one of the parameters of the Wilks lambda distribution is either 1 or 2, e.g.,^[1]

{\frac {1-\Lambda (p,m,1)}{\Lambda (p,m,1)}}\sim {\frac {p}{m-p+1}}F_{p,m-p+1},

and

{\frac {1-{\sqrt {\Lambda (p,m,2)}}}{\sqrt {\Lambda (p,m,2)}}}\sim {\frac {p}{m-p+1}}F_{2p,2(m-p+1)}.

Related Research Articles

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

<span class="mw-page-title-main">Multivariate normal distribution</span> Generalization of the one-dimensional normal distribution to higher dimensions

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

In probability theory and statistics, the chi-squared distribution with $degrees of freedom is the distribution of a sum of the squares of independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution.$

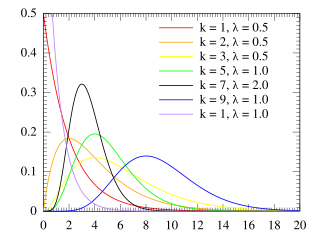
The Erlang distribution is a two-parameter family of continuous probability distributions with support $. The two parameters are:$

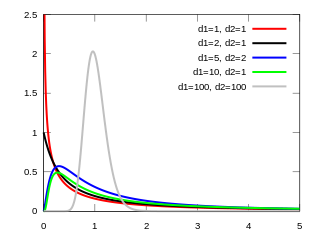
In probability theory and statistics, the F-distribution or F-ratio, also known as Snedecor's F distribution or the Fisher–Snedecor distribution, is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other F-tests.

In statistics, the Wishart distribution is a generalization of the gamma distribution to multiple dimensions. It is named in honor of John Wishart, who first formulated the distribution in 1928. Other names include Wishart ensemble, or Wishart–Laguerre ensemble, or LOE, LUE, LSE.

Hotellings <i>T</i>-squared distribution Type of probability distribution

In statistics, particularly in hypothesis testing, the Hotelling's T-squared distribution (T²), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the F-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's t-distribution. The Hotelling's t-squared statistic (t²) is a generalization of Student's t-statistic that is used in multivariate hypothesis testing.

In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponential distributions spliced together along the abscissa, although the term is also sometimes used to refer to the Gumbel distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. Increments of Laplace motion or a variance gamma process evaluated over the time scale also have a Laplace distribution.

Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes:

To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables.
To derive a lower bound for the marginal likelihood of the observed data. This is typically used for performing model selection, the general idea being that a higher marginal likelihood for a given model indicates a better fit of the data by that model and hence a greater probability that the model in question was the one that generated the data.

<span class="mw-page-title-main">Noncentral chi-squared distribution</span> Noncentral generalization of the chi-squared distribution

In probability theory and statistics, the noncentral chi-squared distribution is a noncentral generalization of the chi-squared distribution. It often arises in the power analysis of statistical tests in which the null distribution is a chi-squared distribution; important examples of such tests are the likelihood-ratio tests.

Bayesian linear regression is a type of conditional modeling in which the mean of one variable is described by a linear combination of other variables, with the goal of obtaining the posterior probability of the regression coefficients and ultimately allowing the out-of-sample prediction of the regressandconditional on observed values of the regressors. The simplest and most widely used version of this model is the normal linear model, in which $given is distributed Gaussian. In this model, and under a particular choice of prior probabilities for the parameters—so-called conjugate priors—the posterior can be found analytically. With more arbitrarily chosen priors, the posteriors generally have to be approximated.$

In statistics, the inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution defined on real-valued positive-definite matrices. In Bayesian statistics it is used as the conjugate prior for the covariance matrix of a multivariate normal distribution.

A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

<span class="mw-page-title-main">Normal-inverse-gamma distribution</span>

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson. The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume. It plays an important role for discrete-stable distributions.

In probability theory and statistics, the noncentral beta distribution is a continuous probability distribution that is a noncentral generalization of the (central) beta distribution.

In probability theory and statistics, the normal-Wishart distribution is a multivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a multivariate normal distribution with unknown mean and precision matrix.

In probability theory and statistics, the normal-inverse-Wishart distribution is a multivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a multivariate normal distribution with unknown mean and covariance matrix.

In statistics, the matrix t-distribution is the generalization of the multivariate t-distribution from vectors to matrices. The matrix t-distribution shares the same relationship with the multivariate t-distribution that the matrix normal distribution shares with the multivariate normal distribution. For example, the matrix t-distribution is the compound distribution that results from sampling from a matrix normal distribution having sampled the covariance matrix of the matrix normal from an inverse Wishart distribution.

In statistics, the complex Wishart distribution is a complex version of the Wishart distribution. It is the distribution of $times the sample Hermitian covariance matrix of zero-mean independent Gaussian random variables. It has support for Hermitian positive definite matrices.$

References

1 2 3 4 5 6 Kanti Mardia, John T. Kent and John Bibby (1979). Multivariate Analysis. Academic Press. ISBN 0-12-471250-9.
↑ M. S. Bartlett (1954). "A Note on the Multiplying Factors for Various $\chi ^{2}$ Approximations". J R Stat Soc Ser B . 16 (2): 296–298. JSTOR 2984057.
↑ C. R. Rao (1951). "An Asymptotic Expansion of the Distribution of Wilks' Criterion". Bulletin de l'Institut International de Statistique . 33: 177–180.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[MKB-1] 1 2 3 4 5 6 Kanti Mardia, John T. Kent and John Bibby (1979). Multivariate Analysis. Academic Press. ISBN 0-12-471250-9.

[2] M. S. Bartlett (1954). "A Note on the Multiplying Factors for Various $\chi ^{2}$ Approximations". J R Stat Soc Ser B . 16 (2): 296–298. JSTOR 2984057.

[3] C. R. Rao (1951). "An Asymptotic Expansion of the Distribution of Wilks' Criterion". Bulletin de l'Institut International de Statistique . 33: 177–180.

[1]

[2]

[3]