
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds, using the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity, as it relates to astronomy and the geodesy of the Earth, and later in the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th century and the 19th century.
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold. It may be described also as the dual bundle to the tangent bundle. This may be generalized to categories with more structure than smooth manifolds, such as complex manifolds, or algebraic varieties or schemes. In the smooth case, any Riemannian metric or symplectic form gives an isomorphism between the cotangent bundle and the tangent bundle, but they are not in general isomorphic in other categories.
In mathematics, a sheaf is a tool for systematically tracking data attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data is well behaved in that it can be restricted to smaller open sets, and also the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set.

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X, which is then called a vector bundle over X.

In mathematics, and particularly topology, a fiber bundle is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space and a product space is defined using a continuous surjective map, , that in small regions of behaves just like a projection from corresponding regions of to . The map , called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space is known as the total space of the fiber bundle, as the base space, and the fiber.

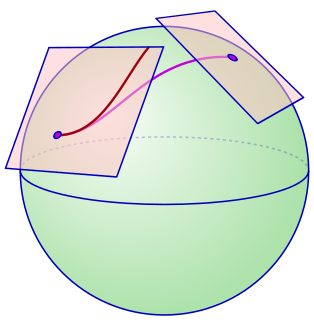
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection, then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection.
In geometry, the notion of a connection makes precise the idea of transporting local geometric objects, such as tangent vectors or tensors in the tangent space, along a curve or family of curves in a parallel and consistent manner. There are various kinds of connections in modern geometry, depending on what sort of data one wants to transport. For instance, an affine connection, the most elementary type of connection, gives a means for parallel transport of tangent vectors on a manifold from one point to another along a curve. An affine connection is typically given in the form of a covariant derivative, which gives a means for taking directional derivatives of vector fields, measuring the deviation of a vector field from being parallel in a given direction.
In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil. Kähler geometry refers to the study of Kähler manifolds, their geometry and topology, as well as the study of structures and constructions that can be performed on Kähler manifolds, such as the existence of special connections like Hermitian Yang–Mills connections, or special metrics such as Kähler–Einstein metrics.
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the geometry of the base manifold using a solder form. Cartan connections describe the geometry of manifolds modelled on homogeneous spaces.
In mathematics, and especially differential geometry and gauge theory, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle P over a smooth manifold M is a particular type of connection which is compatible with the action of the group G.
In differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles.
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms.
In mathematics, an algebraic stack is a vast generalization of algebraic spaces, or schemes, which are foundational for studying moduli theory. Many moduli spaces are constructed using techniques specific to algebraic stacks, such as Artin's representability theorem, which is used to construct the moduli space of pointed algebraic curves and the moduli stack of elliptic curves. Originally, they were introduced by Grothendieck to keep track of automorphisms on moduli spaces, a technique which allows for treating these moduli spaces as if their underlying schemes or algebraic spaces are smooth. But, through many generalizations the notion of algebraic stacks was finally discovered by Michael Artin.
In mathematics, the Gauss–Manin connection is a connection on a certain vector bundle over a base space S of a family of algebraic varieties . The fibers of the vector bundle are the de Rham cohomology groups of the fibers of the family. It was introduced by Yuri Manin (1958) for curves S and by Alexander Grothendieck (1966) in higher dimensions.
In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action.
In mathematics, more precisely in differential geometry, a soldering of a fiber bundle to a smooth manifold is a manner of attaching the fibers to the manifold in such a way that they can be regarded as tangent. Intuitively, soldering expresses in abstract terms the idea that a manifold may have a point of contact with a certain model Klein geometry at each point. In extrinsic differential geometry, the soldering is simply expressed by the tangency of the model space to the manifold. In intrinsic geometry, other techniques are needed to express it. Soldering was introduced in this general form by Charles Ehresmann in 1950.
In mathematics a stack or 2-sheaf is, roughly speaking, a sheaf that takes values in categories rather than sets. Stacks are used to formalise some of the main constructions of descent theory, and to construct fine moduli stacks when fine moduli spaces do not exist.
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaf cohomology is a technique for producing functions with specified properties. Many geometric questions can be formulated as questions about the existence of sections of line bundles or of more general coherent sheaves; such sections can be viewed as generalized functions. Cohomology provides computable tools for producing sections, or explaining why they do not exist. It also provides invariants to distinguish one algebraic variety from another.
This is a glossary of algebraic geometry.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory which admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a physical model of some natural phenomenon.

























