
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi.

In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.
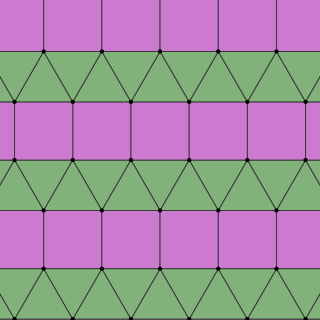
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

In geometry, the snub square tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. Its Schläfli symbol is s{4,4}.

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.

In geometry, a shape is said to be anisohedral if it admits a tiling, but no such tiling is isohedral (tile-transitive); that is, in any tiling by that shape there are two tiles that are not equivalent under any symmetry of the tiling. A tiling by an anisohedral tile is referred to as an anisohedral tiling.
In geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.
In geometry, a uniform honeycomb or uniform tessellation or infinite uniform polytope, is a vertex-transitive honeycomb made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex. Its dimension can be clarified as n-honeycomb for an n-dimensional honeycomb.

A Penrose tiling is an example of an aperiodic tiling. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is aperiodic if it does not contain arbitrarily large periodic regions or patches. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s.

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.

A set of prototiles is aperiodic if copies of the prototiles can be assembled to create tilings, such that all possible tessellation patterns are non-periodic. The aperiodicity referred to is a property of the particular set of prototiles; the various resulting tilings themselves are just non-periodic.

In the mathematical theory of tessellations, the Conway criterion, named for the English mathematician John Horton Conway, is a sufficient rule for when a prototile will tile the plane. It consists of the following requirements: The tile must be a closed topological disk with six consecutive points A, B, C, D, E, and F on the boundary such that:

The Voderberg tiling is a mathematical spiral tiling, invented in 1936 by mathematician Heinz Voderberg (1911-1945). Karl August Reinhardt asked the question of whether there is a tile such that two copies can completely enclose a third copy. Voderberg, his student, answered in the affirmative with Form eines Neunecks eine Lösung zu einem Problem von Reinhardt ["On a nonagon as a solution to a problem of Reinhardt"].

Casey Mann is an American mathematician, specializing in discrete and computational geometry, in particular tessellation and knot theory. He is Professor of Mathematics at University of Washington Bothell, and received the PhD at the University of Arkansas in 2001.




























