
In physics, Kaluza–Klein theory is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the common 4D of space and time and considered an important precursor to string theory. In their setup, the vacuum has the usual 3 dimensions of space and one dimension of time but with another microscopic extra spatial dimension in the shape of a tiny circle. Gunnar Nordström had an earlier, similar idea. But in that case, a fifth component was added to the electromagnetic vector potential, representing the Newtonian gravitational potential, and writing the Maxwell equations in five dimensions.

In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 paper, On the Electrodynamics of Moving Bodies, the theory is presented as being based on just two postulates:
- The laws of physics are invariant (identical) in all inertial frames of reference. This is known as the principle of relativity.
- The speed of light in vacuum is the same for all observers, regardless of the motion of light source or observer. This is known as the principle of light constancy, or the principle of light speed invariance.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. It has become vital in the building of the Standard Model.

Loop quantum gravity (LQG) is a theory of quantum gravity that incorporates matter of the Standard Model into the framework established for the intrinsic quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Albert Einstein's geometric formulation rather than the treatment of gravity as a mysterious mechanism (force). As a theory, LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale on the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.

The Poincaré group, named after Henri Poincaré (1905), was first defined by Hermann Minkowski (1908) as the isometry group of Minkowski spacetime. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our understanding of the most basic fundamentals of physics.

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.
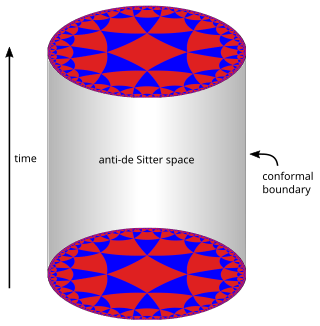
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.

In mathematics and theoretical physics, the term quantum group denotes one of a few different kinds of noncommutative algebras with additional structure. These include Drinfeld–Jimbo type quantum groups, compact matrix quantum groups, and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.
The Gell-Mann matrices, developed by Murray Gell-Mann, are a set of eight linearly independent 3×3 traceless Hermitian matrices used in the study of the strong interaction in particle physics. They span the Lie algebra of the SU(3) group in the defining representation.
In mathematical physics, noncommutative quantum field theory is an application of noncommutative mathematics to the spacetime of quantum field theory that is an outgrowth of noncommutative geometry and index theory in which the coordinate functions are noncommutative. One commonly studied version of such theories has the "canonical" commutation relation:

The Lorentz group is a Lie group of symmetries of the spacetime of special relativity. This group can be realized as a collection of matrices, linear transformations, or unitary operators on some Hilbert space; it has a variety of representations. This group is significant because special relativity together with quantum mechanics are the two physical theories that are most thoroughly established, and the conjunction of these two theories is the study of the infinite-dimensional unitary representations of the Lorentz group. These have both historical importance in mainstream physics, as well as connections to more speculative present-day theories.

The symmetry of a physical system is a physical or mathematical feature of the system that is preserved or remains unchanged under some transformation.
In theoretical physics, the Haag–Łopuszański–Sohnius theorem states that if both commutating and anticommutating generators are considered, then the only way to nontrivially mix spacetime and internal symmetries is through supersymmetry. The anticommutating generators must be spin-1/2 spinors which can additionally admit their own internal symmetry known as R-symmetry. The theorem is a generalization of the Coleman–Mandula theorem to Lie superalgebras. It was proved in 1975 by Rudolf Haag, Jan Łopuszański, and Martin Sohnius as a response to the development of the first supersymmetric field theories by Julius Wess and Bruno Zumino in 1974.

In special relativity, the classical concept of velocity is converted to rapidity to accommodate the limit determined by the speed of light. Velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are almost exactly proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

Shahn Majid is an English pure mathematician and theoretical physicist, trained at Cambridge University and Harvard University and, since 2001, a professor of mathematics at the School of Mathematical Sciences, Queen Mary, University of London.
In physics, Liouville field theory is a two-dimensional conformal field theory whose classical equation of motion is a generalization of Liouville's equation.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems. In application, understanding symmetries can also provide insights on the eigenstates that can be expected. For example, the existence of degenerate states can be inferred by the presence of non commuting symmetry operators or that the non degenerate states are also eigenvectors of symmetry operators.
Bimetric gravity or bigravity refers to two different classes of theories. The first class of theories relies on modified mathematical theories of gravity in which two metric tensors are used instead of one. The second metric may be introduced at high energies, with the implication that the speed of light could be energy-dependent, enabling models with a variable speed of light.

In theoretical physics, the dual graviton is a hypothetical elementary particle that is a dual of the graviton under electric-magnetic duality, as an S-duality, predicted by some formulations of eleven-dimensional supergravity.











































