Trapezoidal distribution

Trapezoidal
	Probability density function
	Cumulative distribution function
Parameters	- lower bound; - level start; - level end; - upper bound;
Support
PDF
CDF
Mean
Variance
Entropy
MGF

Last updated April 11, 2020

In probability theory and statistics, the trapezoidal distribution is a continuous probability distribution the graph of whose probability density function resembles a trapezoid. Likewise, trapezoidal distributions also roughly resemble mesas or plateaus.

Each trapezoidal distribution has a lower bound ${\textstyle a}$ and an upper bound ${\textstyle d}$ , where ${\textstyle a<d}$ , beyond which no values or events on the distribution can occur (i.e. beyond which the probability is always zero). In addition, there are two sharp bending points (non-differentiable discontinuities) within the probability distribution, which we will call $b$ and ${\textstyle c}$ , which occur between ${\textstyle a}$ and ${\textstyle d}$ , such that $a\leq b\leq c\leq d$ .

The image to the right shows a perfectly linear trapezoidal distribution. However, not all trapezoidal distributions are so precisely shaped. In the standard case, where the middle part of the trapezoid is completely flat, and the side ramps are perfectly linear, all of the values between $c$ and ${\textstyle d}$ will occur with equal frequency, and therefore all such points will be modes (local frequency maxima) of the distribution. On the other hand, though, if the middle part of the trapezoid is not completely flat, or if one or both of the side ramps are not perfectly linear, then the trapezoidal distribution in question is a generalized trapezoidal distribution,^[1]^[2] and more complicated and context-dependent rules may apply. The side ramps of a trapezoidal distribution are not required to be symmetric in the general case, just as the sides of trapezoids in geometry are not required to be symmetric.

The non-central moments of the trapezoidal distribution^[3] are

$E[X^{k}]={\frac {2}{d+c-b-a}}{\frac {1}{(k+1)(k+2)}}\left({\frac {d^{k+2}-c^{k+2}}{d-c}}-{\frac {b^{k+2}-a^{k+2}}{b-a}}\right)$

Special cases of the trapezoidal distribution include the uniform distribution (with $a=b$ and ${\textstyle c=d}$ ) and the triangular distribution (with $b=c$ ). Trapezoidal probability distributions seem to not be discussed very often in the literature. The uniform, triangular, Irwin-Hall, Bates, Poisson, normal, bimodal, and multimodal distributions are all more frequently discussed in the literature. This may be because these other (non-trapezoidal) distributions seem to occur more frequently in nature than the trapezoidal distribution does. The normal distribution in particular is especially common in nature, just as one would expect from the central limit theorem.

Related Research Articles

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own boolean-valued outcome: success/yes/true/one or failure/no/false/zero. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

In probability theory, a normaldistribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is

In probability theory and statistics, a probability distribution is a mathematical function that provides the probabilities of occurrence of different possible outcomes in an experiment. In more technical terms, the probability distribution is a description of a random phenomenon in terms of the probabilities of events. For instance, if the random variable $X$ is used to denote the outcome of a coin toss, then the probability distribution of $X$ would take the value 0.5 for $X = heads$ , and 0.5 for $X = tails$ . Examples of random phenomena can include the results of an experiment or survey.

In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.

Negative binomial distribution Probability distribution

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes occurs. For example, we can define rolling a 6 on a die as a success, and rolling any other number as a failure, and ask how many failed rolls will occur before we see the third success. In such a case, the probability distribution of the number of non-6s that appear will be a negative binomial distribution.

Hypergeometric distribution probability distribution

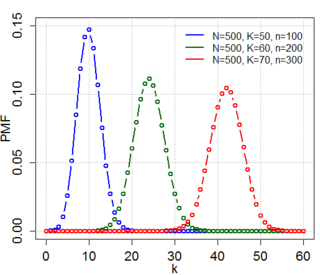
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of $successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.$

In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of exact simulation method. The method works for any distribution in $with a density.$

In probability theory and statistics, the triangular distribution is a continuous probability distribution with lower limit a, upper limit b and mode c, where a < b and a ≤ c ≤ b.

In statistics, the generalized linear model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.

In Bayesian probability theory, if the posterior distributions p(θ | x) are in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood function. For example, the Gaussian family is conjugate to itself with respect to a Gaussian likelihood function: if the likelihood function is Gaussian, choosing a Gaussian prior over the mean will ensure that the posterior distribution is also Gaussian. This means that the Gaussian distribution is a conjugate prior for the likelihood that is also Gaussian. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory. A similar concept had been discovered independently by George Alfred Barnard.

In mathematics, unimodality means possessing a unique mode. More generally, unimodality means there is only a single highest value, somehow defined, of some mathematical object.

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, a and b, which are the minimum and maximum values. The interval can be either closed or open. Therefore, the distribution is often abbreviated U, where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable X under no constraint other than that it is contained in the distribution's support.

In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables.

In probability and statistics, the Irwin–Hall distribution, named after Joseph Oscar Irwin and Philip Hall, is a probability distribution for a random variable defined as the sum of a number of independent random variables, each having a uniform distribution. For this reason it is also known as the uniform sum distribution.

The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "version 1" and "version 2". However this is not a standard nomenclature.

In probability theory and statistics, the Poisson distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.

In mathematical physics and probability and statistics, the Gaussian q-distribution is a family of probability distributions that includes, as limiting cases, the uniform distribution and the normal (Gaussian) distribution. It was introduced by Diaz and Teruel, is a q-analogue of the Gaussian or normal distribution.

In probability and statistics, the Bates distribution, named after Grace Bates, is a probability distribution of the mean of a number of statistically independent uniformly distributed random variables on the unit interval. This distribution is sometimes confused with the Irwin–Hall distribution, which is the distribution of the sum of n independent random variables uniformly distributed from 0 to 1. Thus, the two distributions are simply versions of each other as they only differ in scale.

In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to it being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy, biology, ecology, geology, seismology, physics, economics, image processing, and telecommunications.

References

↑ "Generalized Trapezoidal Distributions" (PDF). Semantic Scholar. March 2003.
↑ van Dorp, J. René; Kotz, Samuel (2003-08-01). "Generalized trapezoidal distributions". Metrika. 58 (1): 85–97. doi:10.1007/s001840200230. ISSN 0026-1335.
↑ Kacker, R. N.; Lawrence, J. F. (2007-02-26). "Trapezoidal and triangular distributions for Type B evaluation of standard uncertainty". Metrologia. 44 (2): 117–127. doi:10.1088/0026-1394/44/2/003. ISSN 0026-1394.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] "Generalized Trapezoidal Distributions" (PDF). Semantic Scholar. March 2003.

[2] van Dorp, J. René; Kotz, Samuel (2003-08-01). "Generalized trapezoidal distributions". Metrika. 58 (1): 85–97. doi:10.1007/s001840200230. ISSN 0026-1335.

[3] Kacker, R. N.; Lawrence, J. F. (2007-02-26). "Trapezoidal and triangular distributions for Type B evaluation of standard uncertainty". Metrologia. 44 (2): 117–127. doi:10.1088/0026-1394/44/2/003. ISSN 0026-1394.

v t e Probability distributions
List
Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher soliton discrete uniform Zipf Zipf–Mandelbrot
Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Flory–Schulz Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta
Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle
Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared noncentral F Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda
Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt
Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Marchenko–Pastur q-exponential q-Gaussian q-Weibull shifted log-logistic Tukey lambda
Mixed continuous-discrete univariate	rectified Gaussian
Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate Laplace multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart
Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham
Degenerate and singular	Degenerate Dirac delta function Singular Cantor
Families	Circular compound Poisson elliptical exponential natural exponential location–scale maximum entropy mixture Pearson Tweedie wrapped

Trapezoidal
Probability density function
Cumulative distribution function
Parameters	$a\;(a<d)$ - lower bound $b\;(a\leq b<c)$ - level start $c\;(b<c\leq d)$ - level end $d\;(c\leq d)$ - upper bound
Support	$x\in [a,d]$
PDF	${\begin{cases}{\frac {2}{d+c-a-b}}{\frac {x-a}{b-a}}&{\text{for }}a\leq x<b\\{\frac {2}{d+c-a-b}}&{\text{for }}b\leq x<c\\{\frac {2}{d+c-a-b}}{\frac {d-x}{d-c}}&{\text{for }}c\leq x\leq d\end{cases}}$
CDF	${\begin{cases}{\frac {1}{d+c-a-b}}{\frac {1}{b-a}}(x-a)^{2}&{\text{for }}a\leq x<b\\{\frac {1}{d+c-a-b}}(2x-a-b)&{\text{for }}b\leq x<c\\1-{\frac {1}{d+c-a-b}}{\frac {1}{d-c}}(d-x)^{2}&{\text{for }}c\leq x\leq d\end{cases}}$
Mean	${\frac {1}{3(d+c-b-a)}}\left({\frac {d^{3}-c^{3}}{d-c}}-{\frac {b^{3}-a^{3}}{b-a}}\right)$
Variance	${\frac {1}{6(d+c-b-a)}}\left({\frac {d^{4}-c^{4}}{d-c}}-{\frac {b^{4}-a^{4}}{b-a}}\right)-\mu ^{2}$
Entropy	${\frac {d-c+b-a}{2(d+c-b-a)}}+\ln \left({\frac {d+c-b-a}{2}}\right)$
MGF	${\frac {2}{d+c-b-a}}{\frac {1}{t^{2}}}\left({\frac {e^{dt}-e^{ct}}{d-c}}-{\frac {e^{bt}-e^{at}}{b-a}}\right)$

Trapezoidal distribution

See also

Related Research Articles

References