
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution, Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution is the distribution of the x-intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero.
The likelihood function is the joint probability of observed data viewed as a function of the parameters of a statistical model.
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions. The larger the scale parameter, the more spread out the distribution.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile. It is a special case of the inverse-gamma distribution. It is a stable distribution.

In probability theory and statistics, the inverse gamma distribution is a two-parameter family of continuous probability distributions on the positive real line, which is the distribution of the reciprocal of a variable distributed according to the gamma distribution.

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.
In probability theory, the "standard" Cauchy distribution is the probability distribution whose probability density function (pdf) is
The normal-inverse Gaussian distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.

In probability theory and statistics, the half-normal distribution is a special case of the folded normal distribution.
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product is a product distribution.
In probability and statistics, a compound probability distribution is the probability distribution that results from assuming that a random variable is distributed according to some parametrized distribution, with the parameters of that distribution themselves being random variables. If the parameter is a scale parameter, the resulting mixture is also called a scale mixture.

In probability theory and statistics, the beta rectangular distribution is a probability distribution that is a finite mixture distribution of the beta distribution and the continuous uniform distribution. The support is of the distribution is indicated by the parameters a and b, which are the minimum and maximum values respectively. The distribution provides an alternative to the beta distribution such that it allows more density to be placed at the extremes of the bounded interval of support. Thus it is a bounded distribution that allows for outliers to have a greater chance of occurring than does the beta distribution.
In probability theory, a subordinator is a stochastic process that is non-negative and whose increments are stationary and independent. Subordinators are a special class of Lévy process that play an important role in the theory of local time. In this context, subordinators describe the evolution of time within another stochastic process, the subordinated stochastic process. In other words, a subordinator will determine the random number of "time steps" that occur within the subordinated process for a given unit of chronological time.
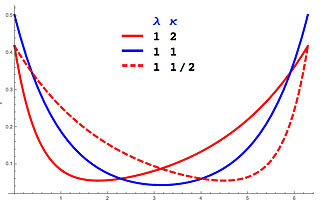
In probability theory and directional statistics, a wrapped asymmetric Laplace distribution is a wrapped probability distribution that results from the "wrapping" of the asymmetric Laplace distribution around the unit circle. For the symmetric case (asymmetry parameter κ = 1), the distribution becomes a wrapped Laplace distribution. The distribution of the ratio of two circular variates (Z) from two different wrapped exponential distributions will have a wrapped asymmetric Laplace distribution. These distributions find application in stochastic modelling of financial data.

The hyperbolastic functions, also known as hyperbolastic growth models, are mathematical functions that are used in medical statistical modeling. These models were originally developed to capture the growth dynamics of multicellular tumor spheres, and were introduced in 2005 by Mohammad Tabatabai, David Williams, and Zoran Bursac. The precision of hyperbolastic functions in modeling real world problems is somewhat due to their flexibility in their point of inflection. These functions can be used in a wide variety of modeling problems such as tumor growth, stem cell proliferation, pharma kinetics, cancer growth, sigmoid activation function in neural networks, and epidemiological disease progression or regression.
An additive process, in probability theory, is a cadlag, continuous in probability stochastic process with independent increments. An additive process is the generalization of a Lévy process. An example of an additive process that is not a Lévy process is a Brownian motion with a time-dependent drift. The additive process was introduced by Paul Lévy in 1937.



























