
In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a sequence of random variables in a probability space, where the index of the sequence often has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance.

In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time.
In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, Shinzo Watanabe, I. Shigekawa, and so on finally completed the foundations.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices, random growth models or physical systems that are subjected to thermal fluctuations.

Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.
In applied probability, a Markov additive process (MAP) is a bivariate Markov process where the future states depends only on one of the variables.
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.
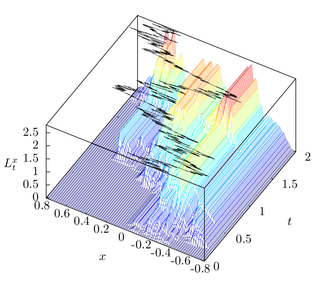
In the mathematical theory of stochastic processes, local time is a stochastic process associated with semimartingale processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level. Local time appears in various stochastic integration formulas, such as Tanaka's formula, if the integrand is not sufficiently smooth. It is also studied in statistical mechanics in the context of random fields.
In the study of stochastic processes, a stochastic process is adapted if information about the value of the process at a given time is available at that same time. An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n. The concept of an adapted process is essential, for instance, in the definition of the Itō integral, which only makes sense if the integrand is an adapted process.
In mathematics, progressive measurability is a property in the theory of stochastic processes. A progressively measurable process, while defined quite technically, is important because it implies the stopped process is measurable. Being progressively measurable is a strictly stronger property than the notion of being an adapted process. Progressively measurable processes are important in the theory of Itô integrals.
In the mathematical field of dynamical systems, a random dynamical system is a dynamical system in which the equations of motion have an element of randomness to them. Random dynamical systems are characterized by a state space S, a set of maps from S into itself that can be thought of as the set of all possible equations of motion, and a probability distribution Q on the set that represents the random choice of map. Motion in a random dynamical system can be informally thought of as a state evolving according to a succession of maps randomly chosen according to the distribution Q.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
In probability theory, a real valued stochastic process X is called a semimartingale if it can be decomposed as the sum of a local martingale and a càdlàg adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itô integral and the Stratonovich integral can be defined.
In probability theory, a Markov kernel is a map that in the general theory of Markov processes plays the role that the transition matrix does in the theory of Markov processes with a finite state space.
In probability theory, an interacting particle system (IPS) is a stochastic process on some configuration space given by a site space, a countably-infinite-order graph and a local state space, a compact metric space . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata.
In the mathematical theory of probability, Blumenthal's zero–one law, named after Robert McCallum Blumenthal, is a statement about the nature of the beginnings of right continuous Feller process. Loosely, it states that any right continuous Feller process on starting from deterministic point has also deterministic initial movement.
The Engelbert–Schmidt zero–one law is a theorem that gives a mathematical criterion for an event associated with a continuous, non-decreasing additive functional of Brownian motion to have probability either 0 or 1, without the possibility of an intermediate value. This zero-one law is used in the study of questions of finiteness and asymptotic behavior for stochastic differential equations. This 0-1 law, published in 1981, is named after Hans-Jürgen Engelbert and the probabilist Wolfgang Schmidt.
In mathematics, stochastic analysis on manifolds or stochastic differential geometry is the study of stochastic analysis over smooth manifolds. It is therefore a synthesis of stochastic analysis and of differential geometry.
The Yamada–Watanabe theorem is a result from probability theory saying that for a large class of stochastic differential equations a weak solution with pathwise uniqueness implies a strong solution and uniqueness in distribution. In its original form, the theorem was stated for -dimensional Itô equations and was proven by the Japanese mathematicians Toshio Yamada and Shinzō Watanabe in 1971. Since then, many generalizations appeared particularly one for general semimartingales by Jean Jacod from 1980.










































