
In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a sequence of random variables, where the index of the sequence has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance.

A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs now." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov.

In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.
In information theory, the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of data compression.

In probability theory, a martingale is a sequence of random variables for which, at a particular time, the conditional expectation of the next value in the sequence is equal to the present value, regardless of all prior values.
Probability is a measure of the likeliness that an event will occur. Probability is used to quantify an attitude of mind towards some proposition whose truth is not certain. The proposition of interest is usually of the form "A specific event will occur." The attitude of mind is of the form "How certain is it that the event will occur?" The certainty that is adopted can be described in terms of a numerical measure, and this number, between 0 and 1 is called the probability. Probability theory is used extensively in statistics, mathematics, science and philosophy to draw conclusions about the likelihood of potential events and the underlying mechanics of complex systems.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.
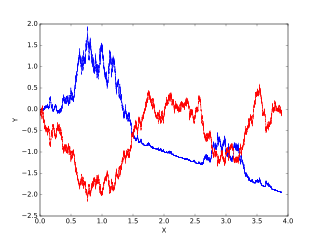
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.
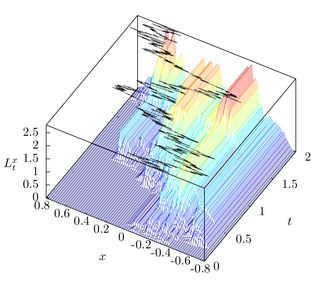
In the mathematical theory of stochastic processes, local time is a stochastic process associated with semimartingale processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level. Local time appears in various stochastic integration formulas, such as Tanaka's formula, if the integrand is not sufficiently smooth. It is also studied in statistical mechanics in the context of random fields.
In probability theory relating to stochastic processes, a Feller process is a particular kind of Markov process.
In mathematics, Doob's martingale inequality, also known as Kolmogorov’s submartingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a submartingale exceeds any given value over a given interval of time. As the name suggests, the result is usually given in the case that the process is a martingale, but the result is also valid for submartingales.
In probability theory, a real valued stochastic process X is called a semimartingale if it can be decomposed as the sum of a local martingale and a càdlàg adapted finite-variation process. Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itô integral and the Stratonovich integral can be defined.
This page lists articles related to probability theory. In particular, it lists many articles corresponding to specific probability distributions. Such articles are marked here by a code of the form (X:Y), which refers to number of random variables involved and the type of the distribution. For example (2:DC) indicates a distribution with two random variables, discrete or continuous. Other codes are just abbreviations for topics. The list of codes can be found in the table of contents.

Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets.
In queueing theory, a discipline within the mathematical theory of probability, a fluid queue is a mathematical model used to describe the fluid level in a reservoir subject to randomly determined periods of filling and emptying. The term dam theory was used in earlier literature for these models. The model has been used to approximate discrete models, model the spread of wildfires, in ruin theory and to model high speed data networks. The model applies the leaky bucket algorithm to a stochastic source.
In probability theory, an interacting particle system (IPS) is a stochastic process on some configuration space given by a site space, a countably-infinite-order graph and a local state space, a compact metric space . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata.

In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy, biology, ecology, geology, seismology, physics, economics, image processing, and telecommunications.








