| Statistics |
|---|
 |
| Part of a series on | ||
| Mathematics | ||
|---|---|---|
 Mathematics Portal | ||
Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory. [1] [2]
Statistical data collection is concerned with the planning of studies, especially with the design of randomized experiments and with the planning of surveys using random sampling. The initial analysis of the data often follows the study protocol specified prior to the study being conducted. The data from a study can also be analyzed to consider secondary hypotheses inspired by the initial results, or to suggest new studies. A secondary analysis of the data from a planned study uses tools from data analysis, and the process of doing this is mathematical statistics.
Data analysis is divided into:
While the tools of data analysis work best on data from randomized studies, they are also applied to other kinds of data. For example, from natural experiments and observational studies, in which case the inference is dependent on the model chosen by the statistician, and so subjective. [3] [4]
The following are some of the important topics in mathematical statistics: [5] [6]
A probability distribution is a function that assigns a probability to each measurable subset of the possible outcomes of a random experiment, survey, or procedure of statistical inference. Examples are found in experiments whose sample space is non-numerical, where the distribution would be a categorical distribution; experiments whose sample space is encoded by discrete random variables, where the distribution can be specified by a probability mass function; and experiments with sample spaces encoded by continuous random variables, where the distribution can be specified by a probability density function. More complex experiments, such as those involving stochastic processes defined in continuous time, may demand the use of more general probability measures.
A probability distribution can either be univariate or multivariate. A univariate distribution gives the probabilities of a single random variable taking on various alternative values; a multivariate distribution (a joint probability distribution) gives the probabilities of a random vector—a set of two or more random variables—taking on various combinations of values. Important and commonly encountered univariate probability distributions include the binomial distribution, the hypergeometric distribution, and the normal distribution. The multivariate normal distribution is a commonly encountered multivariate distribution.
Statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation. [7] Initial requirements of such a system of procedures for inference and induction are that the system should produce reasonable answers when applied to well-defined situations and that it should be general enough to be applied across a range of situations. Inferential statistics are used to test hypotheses and make estimations using sample data. Whereas descriptive statistics describe a sample, inferential statistics infer predictions about a larger population that the sample represents.
The outcome of statistical inference may be an answer to the question "what should be done next?", where this might be a decision about making further experiments or surveys, or about drawing a conclusion before implementing some organizational or governmental policy. For the most part, statistical inference makes propositions about populations, using data drawn from the population of interest via some form of random sampling. More generally, data about a random process is obtained from its observed behavior during a finite period of time. Given a parameter or hypothesis about which one wishes to make inference, statistical inference most often uses:
In statistics, regression analysis is a statistical process for estimating the relationships among variables. It includes many ways for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables. More specifically, regression analysis helps one understand how the typical value of the dependent variable (or 'criterion variable') changes when any one of the independent variables is varied, while the other independent variables are held fixed. Most commonly, regression analysis estimates the conditional expectation of the dependent variable given the independent variables – that is, the average value of the dependent variable when the independent variables are fixed. Less commonly, the focus is on a quantile, or other location parameter of the conditional distribution of the dependent variable given the independent variables. In all cases, the estimation target is a function of the independent variables called the regression function. In regression analysis, it is also of interest to characterize the variation of the dependent variable around the regression function which can be described by a probability distribution.
Many techniques for carrying out regression analysis have been developed. Familiar methods, such as linear regression, are parametric, in that the regression function is defined in terms of a finite number of unknown parameters that are estimated from the data (e.g. using ordinary least squares). Nonparametric regression refers to techniques that allow the regression function to lie in a specified set of functions, which may be infinite-dimensional.
Nonparametric statistics are values calculated from data in a way that is not based on parameterized families of probability distributions. They include both descriptive and inferential statistics. The typical parameters are the expectations, variance, etc. Unlike parametric statistics, nonparametric statistics make no assumptions about the probability distributions of the variables being assessed. [8]
Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. In terms of levels of measurement, non-parametric methods result in "ordinal" data.
As non-parametric methods make fewer assumptions, their applicability is much wider than the corresponding parametric methods. In particular, they may be applied in situations where less is known about the application in question. Also, due to the reliance on fewer assumptions, non-parametric methods are more robust.
One drawback of non-parametric methods is that since they do not rely on assumptions, they are generally less powerful than their parametric counterparts. [9] Low power non-parametric tests are problematic because a common use of these methods is for when a sample has a low sample size. [9] Many parametric methods are proven to be the most powerful tests through methods such as the Neyman–Pearson lemma and the Likelihood-ratio test.
Another justification for the use of non-parametric methods is simplicity. In certain cases, even when the use of parametric methods is justified, non-parametric methods may be easier to use. Due both to this simplicity and to their greater robustness, non-parametric methods are seen by some statisticians as leaving less room for improper use and misunderstanding.
Mathematical statistics is a key subset of the discipline of statistics. Statistical theorists study and improve statistical procedures with mathematics, and statistical research often raises mathematical questions.
Mathematicians and statisticians like Gauss, Laplace, and C. S. Peirce used decision theory with probability distributions and loss functions (or utility functions). The decision-theoretic approach to statistical inference was reinvigorated by Abraham Wald and his successors [10] [11] [12] [13] [14] [15] [16] and makes extensive use of scientific computing, analysis, and optimization; for the design of experiments, statisticians use algebra and combinatorics. But while statistical practice often relies on probability and decision theory, their application can be controversial [4]
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., multivariate random variables. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied.
Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that satisfy the basic principles stated for these different approaches. Within a given approach, statistical theory gives ways of comparing statistical procedures; it can find the best possible procedure within a given context for given statistical problems, or can provide guidance on the choice between alternative procedures.
The following outline is provided as an overview of and topical guide to statistics:
Nonparametric statistics is a type of statistical analysis that makes minimal assumptions about the underlying distribution of the data being studied. Often these models are infinite-dimensional, rather than finite dimensional, as is parametric statistics. Nonparametric statistics can be used for descriptive statistics or statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are evidently violated.
In statistics, probability density estimation or simply density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function. The unobservable density function is thought of as the density according to which a large population is distributed; the data are usually thought of as a random sample from that population.
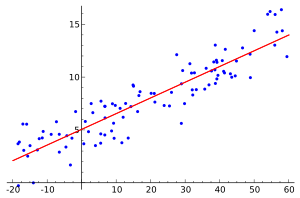
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable and one or more error-free independent variables. The most common form of regression analysis is linear regression, in which one finds the line that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line that minimizes the sum of squared differences between the true data and that line. For specific mathematical reasons, this allows the researcher to estimate the conditional expectation of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters or estimate the conditional expectation across a broader collection of non-linear models.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
A permutation test is an exact statistical hypothesis test making use of the proof by contradiction. A permutation test involves two or more samples. The null hypothesis is that all samples come from the same distribution . Under the null hypothesis, the distribution of the test statistic is obtained by calculating all possible values of the test statistic under possible rearrangements of the observed data. Permutation tests are, therefore, a form of resampling.
The sign test is a statistical test for consistent differences between pairs of observations, such as the weight of subjects before and after treatment. Given pairs of observations for each subject, the sign test determines if one member of the pair tends to be greater than the other member of the pair.
In statistics, resampling is the creation of new samples based on one observed sample. Resampling methods are:
Nonparametric regression is a category of regression analysis in which the predictor does not take a predetermined form but is constructed according to information derived from the data. That is, no parametric form is assumed for the relationship between predictors and dependent variable. Nonparametric regression requires larger sample sizes than regression based on parametric models because the data must supply the model structure as well as the model estimates.
Bootstrapping is a procedure for estimating the distribution of an estimator by resampling one's data or a model estimated from the data. Bootstrapping assigns measures of accuracy to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods.
The term kernel is used in statistical analysis to refer to a window function. The term "kernel" has several distinct meanings in different branches of statistics.
In the statistical analysis of observational data, propensity score matching (PSM) is a statistical matching technique that attempts to estimate the effect of a treatment, policy, or other intervention by accounting for the covariates that predict receiving the treatment. PSM attempts to reduce the bias due to confounding variables that could be found in an estimate of the treatment effect obtained from simply comparing outcomes among units that received the treatment versus those that did not.
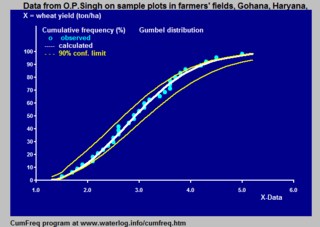
Cumulative frequency analysis is the analysis of the frequency of occurrence of values of a phenomenon less than a reference value. The phenomenon may be time- or space-dependent. Cumulative frequency is also called frequency of non-exceedance.
See Dover reprint, 2004: ISBN 0-486-43912-7
