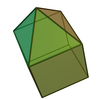
Elongated pyramid

Elongated pyramid
Example: pentagonal form
Faces	n triangles n squares 1 n-gon
Edges	4n
Vertices	2n + 1
Symmetry group	Cnv, [n], (*nn)
Rotation group	Cn, [n]+, (nn)
Dual polyhedron	self-dual
Properties	convex

In geometry, the elongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal prism. Along with the set of pyramids, these figures are topologically self-dual.

There are three elongated pyramids that are Johnson solids:

• Elongated triangular pyramid (J₇),
• Elongated square pyramid (J₈), and
• Elongated pentagonal pyramid (J₉).

Higher forms can be constructed with isosceles triangles.

Forms

	name	faces
	elongated triangular pyramid (J7)	3+1 triangles, 3 squares
	elongated square pyramid (J8)	4 triangles, 4+1 squares
	elongated pentagonal pyramid (J9)	5 triangles, 5 squares, 1 pentagon

See also

• Gyroelongated bipyramid
• Elongated bipyramid
• Gyroelongated pyramid
• Diminished trapezohedron

References

• Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.