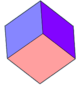
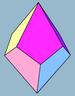
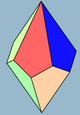
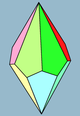
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a "Johnson solid".

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

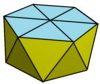
In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an anticube.

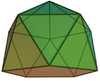
In geometry, an n-gonaltruncated trapezohedron is a polyhedron formed by a n-gonal trapezohedron with n-gonal pyramids truncated from its two polar axis vertices. If the polar vertices are completely truncated (diminished), a trapezohedron becomes an antiprism.

In geometry, the elongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.
In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
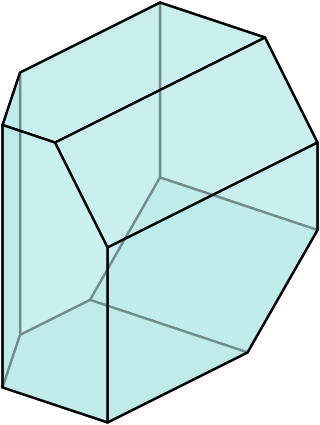
In geometry, an enneahedron is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections. None of them are regular.

In geometry, the elongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal prism. Along with the set of pyramids, these figures are topologically self-dual.

In geometry, the gyroelongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal antiprism.
A hexadecahedron is a polyhedron with 16 faces. No hexadecahedron is regular; hence, the name is ambiguous. There are numerous topologically distinct forms of a hexadecahedron, for example the pentadecagonal pyramid, tetradecagonal prism and heptagonal antiprism.

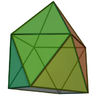
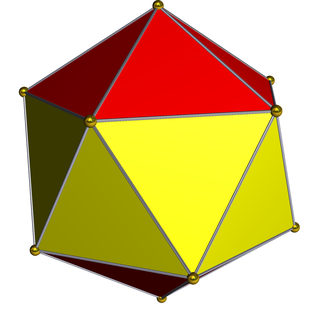
In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".

In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces.
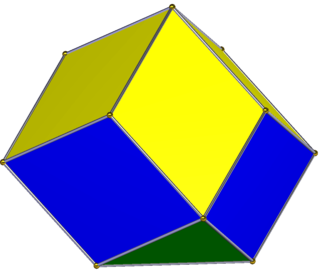
In geometry, a diminished rhombic dodecahedron is a rhombic dodecahedron with one or more vertices removed. This article describes diminishing one 4-valence vertex. This diminishment creates one new square face while 4 rhombic faces are reduced to triangles. It has 13 vertices, 24 edges, and 13 faces. It has C4v symmetry, order 8.