In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a strictly convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two solids with such a property: the first solids are the pyramids, cupolas. and a rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. These solids are named after mathematicians Norman Johnson and Victor Zalgaller.
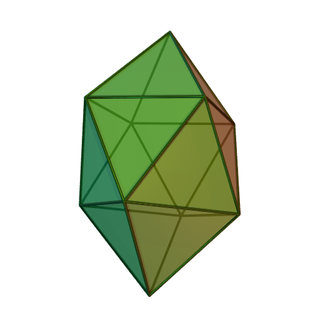
In geometry, the gyroelongated square bipyramid is a polyhedron with 16 triangular faces. it can be constructed from a square antiprism by attaching two equilateral square pyramids to each of its square faces. The same shape is also called hexakaidecadeltahedron, heccaidecadeltahedron, or tetrakis square antiprism; these last names mean a polyhedron with 16 triangular faces. It is an example of deltahedron, and of a Johnson solid.

In geometry, the gyroelongated square pyramid is the Johnson solid that can be constructed by attaching an equilateral square pyramid to a square antiprism. It occurs in chemistry; for example, the square antiprismatic molecular geometry.

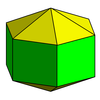
In geometry, the square cupola the cupola with octagonal base. In the case of edges are equal in length, it is the Johnson solid, a convex polyhedron with faces are regular. It can be used to construct many polyhedrons, particularly in other Johnson solids.

In geometry, the elongated square cupola is a polyhedron constructed from an octagonal prism by attaching square cupola onto its base. It is an example of Johnson solid.

In geometry, the square orthobicupola is one of the Johnson solids. As the name suggests, it can be constructed by joining two square cupolae along their octagonal bases, matching like faces. A 45-degree rotation of one cupola before the joining yields a square gyrobicupola.

In geometry, the elongated square pyramid is a convex polyhedron constructed from a cube by attaching an equilateral square pyramid onto one of its faces. It is an example of Johnson solid. It is topologically self-dual.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

In geometry, the elongated pentagonal bipyramid is a polyhedron constructed by attaching two pentagonal pyramids onto the base of a pentagonal prism. It is an example of Johnson solid.

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

In geometry, a bicupola is a solid formed by connecting two cupolae on their bases.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.
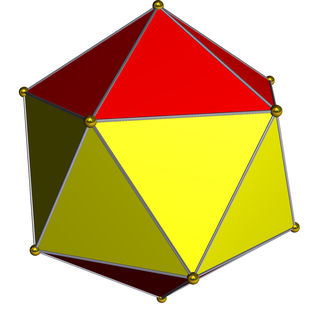
In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.

In geometry, the elongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal prism. Along with the set of pyramids, these figures are topologically self-dual.

In geometry, the gyroelongated pyramids are an infinite set of polyhedra, constructed by adjoining an n-gonal pyramid to an n-gonal antiprism.

In geometry, the elongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to an 2n-gonal prism.
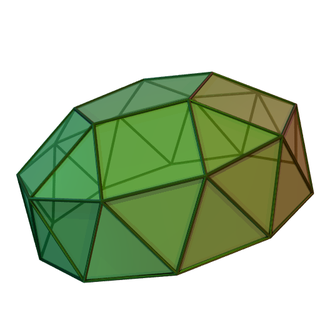
In geometry, the gyroelongated cupolae are an infinite set of polyhedra, constructed by adjoining an n-gonal cupola to an 2n-gonal antiprism.
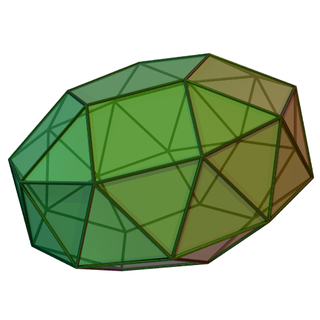
In geometry, the gyroelongated bicupolae are an infinite sets of polyhedra, constructed by adjoining two n-gonal cupolas to an n-gonal Antiprism. The triangular, square, and pentagonal gyroelongated bicupola are three of five Johnson solids which are chiral, meaning that they have a "left-handed" and a "right-handed" form.

In geometry, the elongated bicupolae are two infinite sets of polyhedra, constructed by adjoining two n-gonal cupolas to an n-gonal prism. They have 2n triangles, 4n squares, and 2 n-gon. The ortho forms have the cupola aligned, while gyro forms are counter aligned.

In geometry, a diminished trapezohedron is a polyhedron in an infinite set of polyhedra, constructed by removing one of the polar vertices of a trapezohedron and replacing it by a new face (diminishment). It has one regular n-gonal base face, n triangle faces around the base, and n kites meeting on top. The kites can also be replaced by rhombi with specific proportions.