 | It has been suggested that this article be merged into List of graphs . (Discuss) Proposed since August 2022. |
Some of the finite structures considered in graph theory have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different contexts.
The strongly regular graph on v vertices and rank k is usually denoted srg(v,k,λ,μ).
A symmetric graph is one in which there is a symmetry (graph automorphism) taking any ordered pair of adjacent vertices to any other ordered pair; the Foster census lists all small symmetric 3-regular graphs. Every strongly regular graph is symmetric, but not vice versa.
The complete graph on vertices is often called the -clique and usually denoted , from German komplett. [1]
The complete bipartite graph is usually denoted . For see the section on star graphs. The graph equals the 4-cycle (the square) introduced below.
The cycle graph on vertices is called the n-cycle and usually denoted . It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle, the square, and then several with Greek naming pentagon, hexagon, etc.
The friendship graph Fn can be constructed by joining n copies of the cycle graph C3 with a common vertex. [2]
In graph theory, the term fullerene refers to any 3-regular, planar graph with all faces of size 5 or 6 (including the external face). It follows from Euler's polyhedron formula, V – E + F = 2 (where V, E, F indicate the number of vertices, edges, and faces), that there are exactly 12 pentagons in a fullerene and h = V/2 – 10 hexagons. Therefore V = 20 + 2h; E = 30 + 3h. Fullerene graphs are the Schlegel representations of the corresponding fullerene compounds.
An algorithm to generate all the non-isomorphic fullerenes with a given number of hexagonal faces has been developed by G. Brinkmann and A. Dress. [3] G. Brinkmann also provided a freely available implementation, called fullgen.
The complete graph on four vertices forms the skeleton of the tetrahedron, and more generally the complete graphs form skeletons of simplices. The hypercube graphs are also skeletons of higher-dimensional regular polytopes.
A snark is a bridgeless cubic graph that requires four colors in any proper edge coloring. The smallest snark is the Petersen graph, already listed above.
A star Sk is the complete bipartite graph K1,k. The star S3 is called the claw graph.
The wheel graph Wn is a graph on n vertices constructed by connecting a single vertex to every vertex in an (n − 1)-cycle.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.
In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
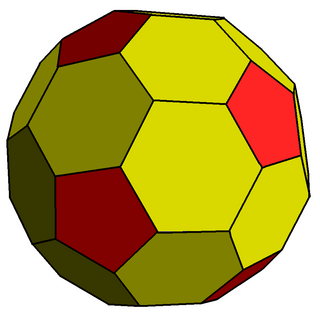
In geometry, the truncated icosahedron is an Archimedean solid, one of 13 convex isogonal nonprismatic solids whose 32 faces are two or more types of regular polygons. It is the only one of these shapes that does not contain triangles or squares. In general usage, the degree of truncation is assumed to be uniform unless specified.
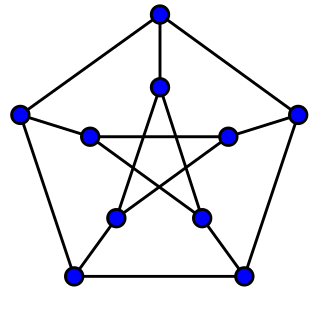
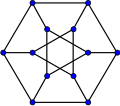
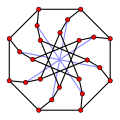
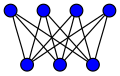
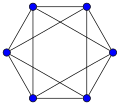
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.
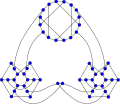
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
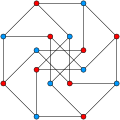
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of finite graphs with perfect matchings. It is a generalization of Hall's marriage theorem from bipartite to arbitrary graphs. It is a special case of the Tutte–Berge formula.
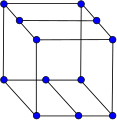
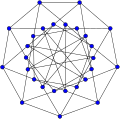
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
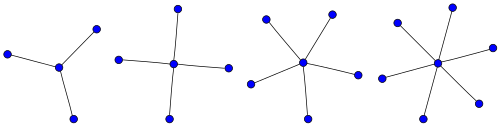
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the subgraph of G induced by all vertices adjacent to v, i.e., the graph composed of the vertices adjacent to v and all edges connecting vertices adjacent to v.
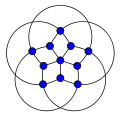
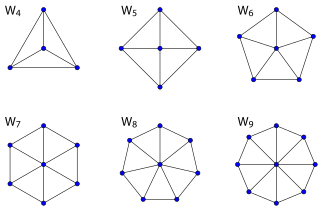
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.
In graph theory, a nowhere-zero flow or NZ flow is a network flow that is nowhere zero. It is intimately connected to coloring planar graphs.
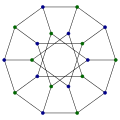
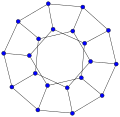
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.
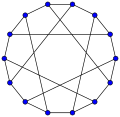
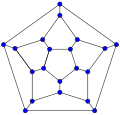
In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges. They were discovered by Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph.
In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.
In topological graph theory, the Petrie dual of an embedded graph is another embedded graph that has the Petrie polygons of the first embedding as its faces.
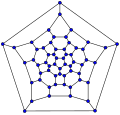
In the mathematical field of graph theory, the 26-fullerene graph is a polyhedral graph with V = 26 vertices and E = 39 edges. Its planar embedding has three hexagonal faces and twelve pentagonal faces. As a planar graph with only pentagonal and hexagonal faces, meeting in three faces per vertex, this graph is a fullerene. The existence of this fullerene has been known since at least 1968.
In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs.
