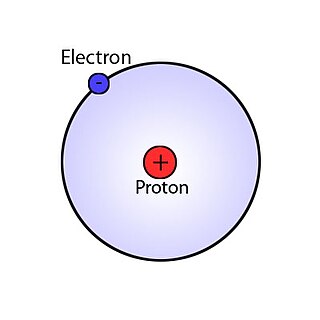
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by α, is a fundamental physical constant which quantifies the strength of the electromagnetic interaction between elementary charged particles.

In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ε (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in response to an applied electric field than a material with low permittivity, thereby storing more energy in the material. In electrostatics, the permittivity plays an important role in determining the capacitance of a capacitor.
Physisorption, also called physical adsorption, is a process in which the electronic structure of the atom or molecule is barely perturbed upon adsorption.
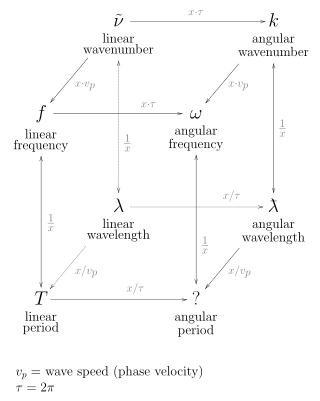
In the physical sciences, the wavenumber, also known as repetency, is the spatial frequency of a wave, measured in cycles per unit distance or radians per unit distance. It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time or radians per unit time.
The Bohr radius is a physical constant, approximately equal to the most probable distance between the nucleus and the electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom. Its value is 5.29177210903(80)×10−11 m.
The hartree, also known as the Hartree energy, is the unit of energy in the atomic units system, named after the British physicist Douglas Hartree. Its CODATA recommended value is Eh = 4.3597447222071(85)×10−18 J = 27.211386245988(53) eV.
The elementary charge, usually denoted by e, is a fundamental physical constant, defined as the electric charge carried by a single proton or, equivalently, the magnitude of the negative electric charge carried by a single electron, which has charge −1 e.
In atomic physics, the Bohr magneton is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by its orbital or spin angular momentum. In SI units, the Bohr magneton is defined as
In spectroscopy, the Rydberg constant, symbol for heavy atoms or for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants according to his model of the atom.

In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.
In quantum physics, Fermi's golden rule is a formula that describes the transition rate from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time and is proportional to the strength of the coupling between the initial and final states of the system as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth.

In physics the Lamb shift, named after Willis Lamb, refers to an anomalous difference in energy between two electron orbitals in a hydrogen atom. The difference was not predicted by theory and it cannot be derived from the Dirac equation, which predicts identical energies. Hence the Lamb shift refers to a deviation from theory seen in the differing energies contained by the 2S1/2 and 2P1/2 orbitals of the hydrogen atom.
The classical electron radius is a combination of fundamental physical quantities that define a length scale for problems involving an electron interacting with electromagnetic radiation. It links the classical electrostatic self-interaction energy of a homogeneous charge distribution to the electron's relativistic mass-energy. According to modern understanding, the electron is a point particle with a point charge and no spatial extent. Nevertheless, it is useful to define a length that characterizes electron interactions in atomic-scale problems. The classical electron radius is given as
The Compton wavelength is a quantum mechanical property of a particle, defined as the wavelength of a photon the energy of which is the same as the rest energy of that particle. It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons.
Vacuum permittivity, commonly denoted ε0, is the value of the absolute dielectric permittivity of classical vacuum. It may also be referred to as the permittivity of free space, the electric constant, or the distributed capacitance of the vacuum. It is an ideal (baseline) physical constant. Its CODATA value is:
In 1927, a year after the publication of the Schrödinger equation, Hartree formulated what are now known as the Hartree equations for atoms, using the concept of self-consistency that Lindsay had introduced in his study of many electron systems in the context of Bohr theory. Hartree assumed that the nucleus together with the electrons formed a spherically symmetric field. The charge distribution of each electron was the solution of the Schrödinger equation for an electron in a potential , derived from the field. Self-consistency required that the final field, computed from the solutions, was self-consistent with the initial field, and he thus called his method the self-consistent field method.
The Planck constant, or Planck's constant, denoted by , is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum.
The isotopic shift is the shift in various forms of spectroscopy that occurs when one nuclear isotope is replaced by another.
The Mott–Bethe formula is an approximation used to calculate atomic electron scattering form factors, , from atomic X-ray scattering form factors, . The formula was derived independently by Hans Bethe and Neville Mott both in 1930, and simply follows from applying the first Born approximation for the scattering of electrons via the Coulomb interaction together with the Poisson equation for the charge density of an atom in the Fourier domain. Following the first Born approximation,