
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.

Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term can also refer to the computation of integrals.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations, including fluid mechanics, acoustics, electromagnetics, fracture mechanics, and contact mechanics.
In electrical engineering, a differential-algebraic system of equations (DAE) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system. In mathematics these are examples of differential algebraic varieties and correspond to ideals in differential polynomial rings.

In computational modelling, multiphysics simulation is defined as the simultaneous simulation of different aspects of a physical system or systems and the interactions among them. For example, simultaneous simulation of the physical stress on an object, the temperature distribution of the object and the thermal expansion which leads to the variation of the stress and temperature distributions would be considered a multiphysics simulation. Multiphysics simulation is related to multiscale simulation, which is the simultaneous simulation of a single process on either multiple time or distance scales.

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, namely that several different initial chaotic conditions evolve in phase space in a way that never repeats, so all chaos is unpredictable. This underscores that chaotic systems can be completely deterministic and yet still be inherently unpredictable over long periods of time. Because chaos continually increases in systems, we cannot predict the future of systems well. E.g., even the small flap of a butterfly’s wings could set the world on a vastly different trajectory, such as by causing a hurricane. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.
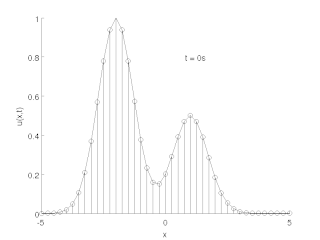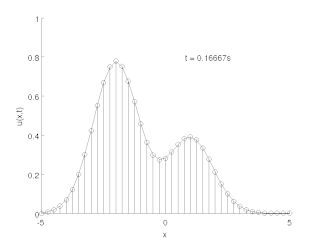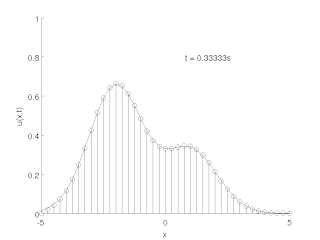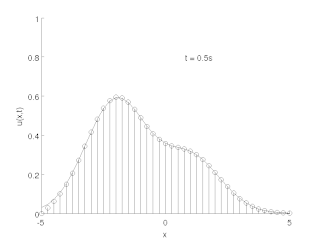
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. By reducing a PDE to a single continuous dimension, the method of lines allows solutions to be computed via methods and software developed for the numerical integration of ordinary differential equations (ODEs) and differential-algebraic systems of equations (DAEs). Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.
Finite element exterior calculus (FEEC) is a mathematical framework that formulates finite element methods using chain complexes. Its main application has been a comprehensive theory for finite element methods in computational electromagnetism, computational solid and fluid mechanics. FEEC was developed in the early 2000s by Douglas N. Arnold, Richard S. Falk and Ragnar Winther, among others. Finite element exterior calculus is sometimes called as an example of a compatible discretization technique, and bears similarities with discrete exterior calculus, although they are distinct theories.
Dynamic simulation is the use of a computer program to model the time-varying behavior of a dynamical system. The systems are typically described by ordinary differential equations or partial differential equations. A simulation run solves the state-equation system to find the behavior of the state variables over a specified period of time. The equation is solved through numerical integration methods to produce the transient behavior of the state variables. Simulation of dynamic systems predicts the values of model-system state variables, as they are determined by the past state values. This relationship is found by creating a model of the system.
In contact mechanics, the term unilateral contact, also called unilateral constraint, denotes a mechanical constraint which prevents penetration between two rigid/flexible bodies. Constraints of this kind are omnipresent in non-smooth multibody dynamics applications, such as granular flows, legged robot, vehicle dynamics, particle damping, imperfect joints, or rocket landings. In these applications, the unilateral constraints result in impacts happening, therefore requiring suitable methods to deal with such constraints.

In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with other DE, its unknown(s) consists of one function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equations which may be with respect to more than one independent variable.
Exponential integrators are a class of numerical methods for the solution of ordinary differential equations, specifically initial value problems. This large class of methods from numerical analysis is based on the exact integration of the linear part of the initial value problem. Because the linear part is integrated exactly, this can help to mitigate the stiffness of a differential equation. Exponential integrators can be constructed to be explicit or implicit for numerical ordinary differential equations or serve as the time integrator for numerical partial differential equations.
Geometric mechanics is a branch of mathematics applying particular geometric methods to many areas of mechanics, from mechanics of particles and rigid bodies to fluid mechanics to control theory.
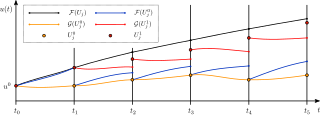
Parareal is a parallel algorithm from numerical analysis and used for the solution of initial value problems. It was introduced in 2001 by Lions, Maday and Turinici. Since then, it has become one of the most widely studied parallel-in-time integration methods.
Peter John Olver is a British-American mathematician working in differential geometry.
Hans Zanna Munthe-Kaas is a Norwegian mathematician at the University of Bergen, and UiT The Arctic University of Norway working in the area of computational mathematics in the borderland between pure and applied mathematics and computer science.
Probabilistic numerics is an active field of study at the intersection of applied mathematics, statistics, and machine learning centering on the concept of uncertainty in computation. In probabilistic numerics, tasks in numerical analysis such as finding numerical solutions for integration, linear algebra, optimization and simulation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.

Klaus Schmitt is an American mathematician doing research in nonlinear differential equations, and nonlinear analysis.







