In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.
In geometry, a cuboid is a quadrilateral-faced convex hexahedron, a polyhedron with six faces.

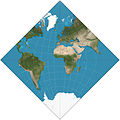
The Dymaxion map or Fuller map is a projection of a world map onto the surface of an icosahedron, which can be unfolded and flattened to two dimensions. The flat map is heavily interrupted in order to preserve shapes and sizes.

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of n edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q). Dihedra have also been called bihedra, flat polyhedra, or doubly covered polygons.

The Peirce quincuncial projection is the conformal map projection from the sphere to an unfolded square dihedron, developed by Charles Sanders Peirce in 1879. Each octant projects onto an isosceles right triangle, and these are arranged into a square. The name quincuncial refers to this arrangement: the north pole at the center and quarters of the south pole in the corners form a quincunx pattern like the pips on the five face of a traditional die. The projection has the distinctive property that it forms a seamless square tiling of the plane, conformal except at four singular points along the equator.

Bernard Joseph Stanislaus Cahill, American cartographer and architect, was the inventor of the octahedral "Butterfly Map". An early proponent of the San Francisco Civic Center, he also designed hotels, factories and mausoleums like the Columbarium of San Francisco.

In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.

The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection.

The Adams hemisphere-in-a-square is a conformal map projection for a hemisphere. It is a transverse version of the Peirce quincuncial projection, and is named after American cartographer Oscar S. Adams, who published it in 1925. When it is used to represent the entire sphere it is known as the Adams doubly periodic projection. Like many conformal projections, conformality fails at certain points, in this case at the four corners.
In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth is preserved in the image of the projection; that is, the projection is a conformal map in the mathematical sense. For example, if two roads cross each other at a 39° angle, their images on a map with a conformal projection cross at a 39° angle.
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron – hence the "hemi" prefix.
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids.

The Waterman "Butterfly" World Map is a map projection created by Steve Waterman. Waterman first published a map in this arrangement in 1996. The arrangement is an unfolding of a polyhedral globe with the shape of a truncated octahedron, evoking the butterfly map principle first developed by Bernard J.S. Cahill (1866–1944) in 1909. Cahill and Waterman maps can be shown in various profiles, typically linked at the north Pacific or north Atlantic oceans.

The Cahill–Keyes projection is a polyhedral compromise map projection first proposed by Gene Keyes in 1975. The projection is a refinement of an earlier 1909 projection by Bernard Cahill. The projection was designed to achieve a number of desirable characteristics, namely symmetry of component maps (octants), scalability allowing the map to continue to work well even at high resolution, uniformity of geocells, metric-based joining edges, minimized distortion compared to a globe, and an easily understood orientation to enhance general usability and teachability.

A discrete global grid (DGG) is a mosaic that covers the entire Earth's surface. Mathematically it is a space partitioning: it consists of a set of non-empty regions that form a partition of the Earth's surface. In a usual grid-modeling strategy, to simplify position calculations, each region is represented by a point, abstracting the grid as a set of region-points. Each region or region-point in the grid is called a cell.

AuthaGraph is an approximately equal-area world map projection invented by Japanese architect Hajime Narukawa in 1999. The map is made by equally dividing a spherical surface into 96 triangles, transferring it to a tetrahedron while maintaining area proportions, and unfolding it in the form of a rectangle: it is a polyhedral map projection. The map substantially preserves sizes and shapes of all continents and oceans while it reduces distortions of their shapes, as inspired by the Dymaxion map. The projection does not have some of the major distortions of the Mercator projection, like the expansion of countries in far northern latitudes, and allows for Antarctica to be displayed accurately and in whole. Triangular world maps are also possible using the same method. The name is derived from "authalic" and "graph".

The octant projection or octants projection, is a type of map projection proposed the first time, in 1508, by Leonardo da Vinci in his Codex Atlanticus. Leonardo's authorship would be demonstrated by Christopher Tyler, who stated "For those projections dated later than 1508, his drawings should be effectively considered the original precursors."

The Lee conformal world in a tetrahedron is a polyhedral, conformal map projection that projects the globe onto a tetrahedron using Dixon elliptic functions. It is conformal everywhere except for the four singularities at the vertices of the polyhedron. Because of the nature of polyhedra, this map projection can be tessellated infinitely in the plane. It was developed by Laurence Patrick Lee in 1965.

In map projections, an interruption is any place where the globe has been split. All map projections are interrupted at at least one point. Typical world maps are interrupted along an entire meridian. In that typical case, the interruption forms an east/west boundary, even though the globe has no boundaries.