
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each one. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
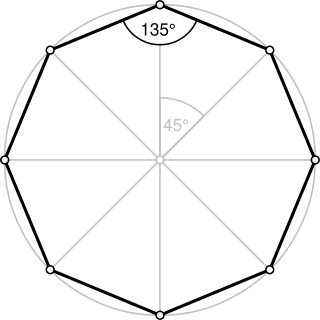
In geometry, an octagon is an eight-sided polygon or 8-gon.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6}.

In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares around every vertex.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated trihexagonal tiling is one of eight semiregular tilings of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex. It has Schläfli symbol of tr{3,6}.

In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.

In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.
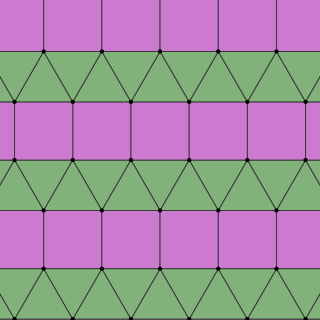
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

In geometry, the tetrakis square tiling is a tiling of the Euclidean plane. It is a square tiling with each square divided into four isosceles right triangles from the center point, forming an infinite arrangement of lines. It can also be formed by subdividing each square of a grid into two triangles by a diagonal, with the diagonals alternating in direction, or by overlaying two square grids, one rotated by 45 degrees from the other and scaled by a factor of √2.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.

A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.

In geometry, the rhombitetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{6,4}. It can be seen as constructed as a rectified tetrahexagonal tiling, r{6,4}, as well as an expanded order-4 hexagonal tiling or expanded order-6 square tiling.

In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.

In geometry, the rhombitetraoctagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{8,4}. It can be seen as constructed as a rectified tetraoctagonal tiling, r{8,4}, as well as an expanded order-4 octagonal tiling or expanded order-8 square tiling.









































