This article needs additional citations for verification .(December 2009) |
Game theory is the branch of mathematics in which games are studied: that is, models describing human behaviour. This is a glossary of some terms of the subject.
This article needs additional citations for verification .(December 2009) |
Game theory is the branch of mathematics in which games are studied: that is, models describing human behaviour. This is a glossary of some terms of the subject.
is an element of .
an element of , is a tuple of strategies for all players other than i.
A game in normal form is a function:
Given the tuple of strategies chosen by the players, one is given an allocation of payments (given as real numbers).
A further generalization can be achieved by splitting the game into a composition of two functions:
the outcome function of the game (some authors call this function "the game form"), and:
the allocation of payoffs (or preferences) to players, for each outcome of the game.
This is given by a tree, where at each vertex of the tree a different player has the choice of choosing an edge. The outcome set of an extensive form game is usually the set of tree leaves.
A game in which players are allowed to form coalitions (and to enforce coalitionary discipline). A cooperative game is given by stating a value for every coalition:
It is always assumed that the empty coalition gains nil. Solution concepts for cooperative games usually assume that the players are forming the grand coalition, whose value is then divided among the players to give an allocation.
A Simple game is a simplified form of a cooperative game, where the possible gain is assumed to be either '0' or '1'. A simple game is couple (N, W), where W is the list of "winning" coalitions, capable of gaining the loot ('1'), and N is the set of players.

In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material. Thus, the larger the optical depth, the smaller the amount of transmitted radiant power through the material. Spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.

In probability and statistics, Student's t distribution is a continuous probability distribution that generalizes the standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
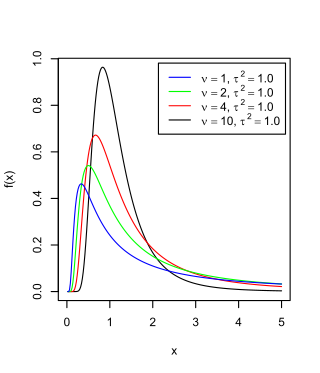
The scaled inverse chi-squared distribution is the distribution for x = 1/s2, where s2 is a sample mean of the squares of ν independent normal random variables that have mean 0 and inverse variance 1/σ2 = τ2. The distribution is therefore parametrised by the two quantities ν and τ2, referred to as the number of chi-squared degrees of freedom and the scaling parameter, respectively.
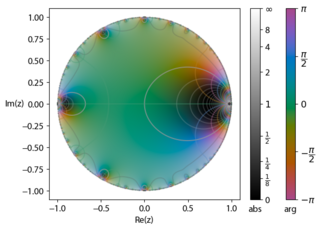
In mathematics, the Euler function is given by
In probability theory, the central limit theorem says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingales, which are stochastic processes where the change in the value of the process from time t to time t + 1 has expectation zero, even conditioned on previous outcomes.
In mathematical physics, the gamma matrices, also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin particles. Gamma matrices were introduced by Dirac in 1928.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In the Newman–Penrose (NP) formalism of general relativity, Weyl scalars refer to a set of five complex scalars which encode the ten independent components of the Weyl tensor of a four-dimensional spacetime.
In 3-dimensional topology, a part of the mathematical field of geometric topology, the Casson invariant is an integer-valued invariant of oriented integral homology 3-spheres, introduced by Andrew Casson.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p. In a normal coordinate system, the Christoffel symbols of the connection vanish at the point p, thus often simplifying local calculations. In normal coordinates associated to the Levi-Civita connection of a Riemannian manifold, one can additionally arrange that the metric tensor is the Kronecker delta at the point p, and that the first partial derivatives of the metric at p vanish.
In statistics, the multivariate t-distribution is a multivariate probability distribution. It is a generalization to random vectors of the Student's t-distribution, which is a distribution applicable to univariate random variables. While the case of a random matrix could be treated within this structure, the matrix t-distribution is distinct and makes particular use of the matrix structure.
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.
In mathematics, Maass forms or Maass wave forms are studied in the theory of automorphic forms. Maass forms are complex-valued smooth functions of the upper half plane, which transform in a similar way under the operation of a discrete subgroup of as modular forms. They are eigenforms of the hyperbolic Laplace operator defined on and satisfy certain growth conditions at the cusps of a fundamental domain of . In contrast to modular forms, Maass forms need not be holomorphic. They were studied first by Hans Maass in 1949.
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.
In the Newman–Penrose (NP) formalism of general relativity, independent components of the Ricci tensors of a four-dimensional spacetime are encoded into seven Ricci scalars which consist of three real scalars , three complex scalars and the NP curvature scalar . Physically, Ricci-NP scalars are related with the energy–momentum distribution of the spacetime due to Einstein's field equation.
Stochastic portfolio theory (SPT) is a mathematical theory for analyzing stock market structure and portfolio behavior introduced by E. Robert Fernholz in 2002. It is descriptive as opposed to normative, and is consistent with the observed behavior of actual markets. Normative assumptions, which serve as a basis for earlier theories like modern portfolio theory (MPT) and the capital asset pricing model (CAPM), are absent from SPT.
The streamline upwind Petrov–Galerkin pressure-stabilizing Petrov–Galerkin formulation for incompressible Navier–Stokes equations can be used for finite element computations of high Reynolds number incompressible flow using equal order of finite element space by introducing additional stabilization terms in the Navier–Stokes Galerkin formulation.