The Gibbard–Satterthwaite theorem is a theorem in voting theory. It was first conjectured by the philosopher Michael Dummett and the mathematician Robin Farquharson in 1961 and then proved independently by the philosopher Allan Gibbard in 1973 and economist Mark Satterthwaite in 1975. It deals with deterministic ordinal electoral systems that choose a single winner, and shows that for every voting rule of this form, at least one of the following three things must hold:
- The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or
- The rule limits the possible outcomes to two alternatives only; or
- The rule is not straightforward, i.e. there is no single always-best strategy.
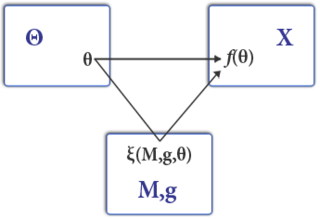
Mechanism design is a branch of economics, social choice theory, and game theory that deals with designing games to implement a given social choice function. Because it starts at the end of the game and then works backwards to find a game that implements it, it is sometimes called reverse game theory.
In mechanism design, a strategyproof (SP) mechanism is a game in which each player has a weakly-dominant strategy, so that no player can gain by "spying" over the other players to know what they are going to play. When the players have private information, and the strategy space of each player consists of the possible information values, a truthful mechanism is a game in which revealing the true information is a weakly-dominant strategy for each player. An SP mechanism is also called dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility.
In economics and game theory, complete information is an economic situation or game in which knowledge about other market participants or players is available to all participants. The utility functions, payoffs, strategies and "types" of players are thus common knowledge. Complete information is the concept that each player in the game is aware of the sequence, strategies, and payoffs throughout gameplay. Given this information, the players have the ability to plan accordingly based on the information to maximize their own strategies and utility at the end of the game.
Social choice theory or social choice is a branch of welfare economics that studies the processes of collective decision-making. Social choice incorporates insights from economics, mathematics, and game theory to find the best ways to combine individual opinions, preferences, or beliefs into a single coherent measure of the quality of different outcomes, called a social welfare function. Social choice theory includes the closely-related field of voting theory, and is strongly tied to the field of mechanism design, which can be thought of as the combination of social choice with game theory.
In game theory, folk theorems are a class of theorems describing an abundance of Nash equilibrium payoff profiles in repeated games. The original Folk Theorem concerned the payoffs of all the Nash equilibria of an infinitely repeated game. This result was called the Folk Theorem because it was widely known among game theorists in the 1950s, even though no one had published it. Friedman's (1971) Theorem concerns the payoffs of certain subgame-perfect Nash equilibria (SPE) of an infinitely repeated game, and so strengthens the original Folk Theorem by using a stronger equilibrium concept: subgame-perfect Nash equilibria rather than Nash equilibria.

A double auction is a process of buying and selling goods with multiple sellers and multiple buyers. Potential buyers submit their bids and potential sellers submit their ask prices to the market institution, and then the market institution chooses some price p that clears the market: all the sellers who asked less than p sell and all buyers who bid more than p buy at this price p. Buyers and sellers that bid or ask for exactly p are also included. A common example of a double auction is stock exchange.
A mechanism is called incentive-compatible (IC) or truthful if every participant can achieve their own best outcome by acting according to their true preferences. For example, there is incentive compatibility if high-risk clients are better off in identifying themselves as high-risk to insurance firms, who only sell discounted insurance to high-risk clients. Likewise, they would be worse off if they pretend to be low-risk. Low-risk clients who pretend to be high-risk would also be worse off.

A first-price sealed-bid auction (FPSBA) is a common type of auction. It is also known as blind auction. In this type of auction, all bidders simultaneously submit sealed bids so that no bidder knows the bid of any other participant. The highest bidder pays the price that was submitted.
Implementation theory is an area of research in game theory concerned with whether a class of mechanisms can be designed whose equilibrium outcomes implement a given set of normative goals or welfare criteria.

Revenue equivalence is a concept in auction theory that states that given certain conditions, any mechanism that results in the same outcomes also has the same expected revenue.

Jean-François Mertens was a Belgian game theorist and mathematical economist.

Arunava Sen is a professor of economics at the Indian Statistical Institute. He works on Game Theory, Social Choice Theory, Mechanism Design, Voting and Auctions.
In mechanism design, a Vickrey–Clarke–Groves (VCG) mechanism is a generic truthful mechanism for achieving a socially-optimal solution. It is a generalization of a Vickrey–Clarke–Groves auction. A VCG auction performs a specific task: dividing items among people. A VCG mechanism is more general: it can be used to select any outcome out of a set of possible outcomes.
In mechanism design, implementability is a property of a social choice function. It means that there is an incentive-compatible mechanism that attains ("implements") this function. There are several degrees of implementability, corresponding to the different degrees of incentive-compatibility, e.g:
In mechanism design, monotonicity is a property of a social choice function. It is a necessary condition for being able to implement the function using a strategyproof mechanism. Its verbal description is:
If changing one agent's type changes the outcome under the social choice function, then the resulting difference in utilities of the new and original outcomes evaluated at the new type of this agent must be at least as much as this difference in utilities evaluated at the original type of this agent.
A sequential auction is an auction in which several items are sold, one after the other, to the same group of potential buyers. In a sequential first-price auction (SAFP), each individual item is sold using a first price auction, while in a sequential second-price auction (SASP), each individual item is sold using a second price auction.

The Price of Anarchy (PoA) is a concept in game theory and mechanism design that measures how the social welfare of a system degrades due to selfish behavior of its agents. It has been studied extensively in various contexts, particularly in auctions.
Guoqiang Tian is a Chinese-American economist. He is the Alfred F. Chalk Professor of Economics at Texas A&M University. He is Honorary Dean of Institute for Advanced Research at Shanghai University of Finance and Economics.
Truthful resource allocation is the problem of allocating resources among agents with different valuations over the resources, such that agents are incentivized to reveal their true valuations over the resources.







