 | The article's lead section may need to be rewritten.(October 2023) |
 120-cell     |  600-cell |
In 4-dimensional geometry, there are 15 uniform polytopes with H4 symmetry. Two of these, the 120-cell and 600-cell, are regular.
| The article's lead section may need to be rewritten.(October 2023) |
| 120-cell | 600-cell |
In 4-dimensional geometry, there are 15 uniform polytopes with H4 symmetry. Two of these, the 120-cell and 600-cell, are regular.
Each can be visualized as symmetric orthographic projections in Coxeter planes of the H4 Coxeter group, and other subgroups.
The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.
| # | Name | Coxeter plane projections | Schlegel diagrams | Net | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | [20] | H4 [30] | H3 [10] | A3 [4] | A2 [3] | Dodecahedron centered | Tetrahedron centered | |||
| 1 | 120-cell {5,3,3} |  |  |  |  |  |  |  |  | |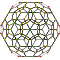
| 2 | rectified 120-cell r{5,3,3} |  |  |  |  |  |  |  |  | |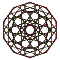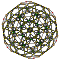
| 3 | rectified 600-cell r{3,3,5} |  |  |  |  |  |  |  |  | |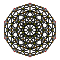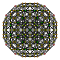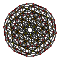
| 4 | 600-cell {3,3,5} |  |  |  |  |  |  |  |  |  |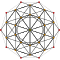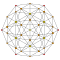
| 5 | truncated 120-cell t{5,3,3} |  |  |  |  |  |  |  |  | |
| 6 | cantellated 120-cell rr{5,3,3} |  |  |  |  |  | ||||
| 7 | runcinated 120-cell (also runcinated 600-cell) t0,3{5,3,3} |  |  |  |  |  | ||||
| 8 | bitruncated 120-cell (also bitruncated 600-cell) t1,2{5,3,3} |  |  |  |  |  | ||||
| 9 | cantellated 600-cell t0,2{3,3,5} |  |  |  |  |  |  |  |  | |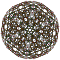
| 10 | truncated 600-cell t{3,3,5} |  |  |  |  |  |  |  |  | |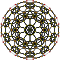
| 11 | cantitruncated 120-cell tr{5,3,3} |  |  |  |  |  | ||||
| 12 | runcitruncated 120-cell t0,1,3{5,3,3} |  |  |  |  |  | ||||
| 13 | runcitruncated 600-cell t0,1,3{3,3,5} |  |  |  |  |  | ||||
| 14 | cantitruncated 600-cell tr{3,3,5} |  |  |  |  |  | ||||
| 15 | omnitruncated 120-cell (also omnitruncated 600-cell) t0,1,2,3{5,3,3} |  |  |  |  |  | ||||
| # | Name | Coxeter plane projections | Schlegel diagrams | Net | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | [20] | H4 [30] | H3 [10] | A3 [4] | A2 [3] | Dodecahedron centered | Tetrahedron centered | |||
| 16 | 20-diminished 600-cell (grand antiprism) |  |  |  | ||||||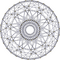
| 17 | 24-diminished 600-cell (snub 24-cell) |  |  |  |  | |||||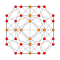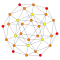
| 18 Nonuniform | Bi-24-diminished 600-cell |  |  |  | ||||||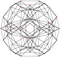
| 19 Nonuniform | 120-diminished rectified 600-cell |  | ||||||||
The coordinates of uniform polytopes from the H4 family are complicated. The regular ones can be expressed in terms of the golden ratio φ = (1 + √5)/2 and σ = (3√5 + 1)/2. Coxeter expressed them as 5-dimensional coordinates. [1]
| n | 120-cell | 600-cell |
|---|---|---|
| 4D | The 600 vertices of the 120-cell include all permutations of [2]
and all even permutations of
| The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = (1+√5)/2 is the golden ratio), can be given as follows: 16 vertices of the form [3]
and 8 vertices obtained from
The remaining 96 vertices are obtained by taking even permutations of
|
| 5D | Zero-sum permutation:
| Zero-sum permutation:
|
In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.
In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.
In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.
In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.
In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.
In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.
In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.
In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.
In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.
In five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation (runcination) of the regular 5-orthoplex.
In seven-dimensional geometry, a hexic 7-cube is a convex uniform 7-polytope, constructed from the uniform 7-demicube. There are 16 unique forms.
In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.
In 4-dimensional geometry, there are 15 uniform 4-polytopes with B4 symmetry. There are two regular forms, the tesseract and 16-cell, with 16 and 8 vertices respectively.
In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D4 symmetry, all are shared with higher symmetry constructions in the B4 or F4 symmetry families. there is also one half symmetry alternation, the snub 24-cell.