| Rectified 600-cell | |
|---|---|
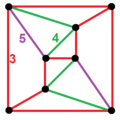
 Schlegel diagram, shown as Birectified 120-cell, with 119 icosahedral cells colored | |
| Type | Uniform 4-polytope |
| Uniform index | 34 |
| Schläfli symbol | t1{3,3,5} or r{3,3,5} |
| Coxeter-Dynkin diagram | |
| Cells | 600 (3.3.3.3) 120 {3,5} |
| Faces | 1200+2400 {3} |
| Edges | 3600 |
| Vertices | 720 |
| Vertex figure |  pentagonal prism |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex, vertex-transitive, edge-transitive |
In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.
Contents
- Semiregular polytope
- Alternate names
- Images
- Related polytopes
- Diminished rectified 600-cell
- H4 family
- Pentagonal prism vertex figures
- References
- External links
Containing the cell realms of both the regular 120-cell and the regular 600-cell, it can be considered analogous to the polyhedron icosidodecahedron, which is a rectified icosahedron and rectified dodecahedron.
The vertex figure of the rectified 600-cell is a uniform pentagonal prism.