In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

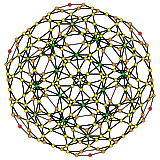
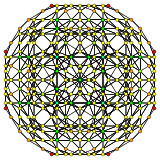
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also called a C600, hexacosichoron and hexacosihedroid.

In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4-simplex (Coxeter's polytope), the simplest possible convex regular 4-polytope (four-dimensional analogue of a Platonic solid), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The pentachoron is a four dimensional pyramid with a tetrahedral base.

In four-dimensional geometry, a 16-cell is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid.

In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.

In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10 vertices. Each vertex is surrounded by 3 octahedra and 2 tetrahedra; the vertex figure is a triangular prism.

In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.
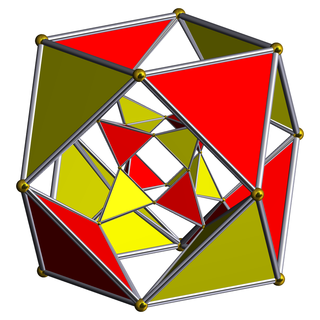
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.

In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In six-dimensional geometry, a rectified 6-orthoplex is a convex uniform 6-polytope, being a rectification of the regular 6-orthoplex.

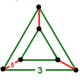
In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.

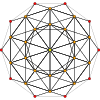
In 4-dimensional geometry, there are 15 uniform 4-polytopes with B4 symmetry. There are two regular forms, the tesseract, and 16-cell with 16 and 8 vertices respectively.

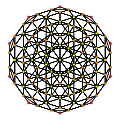
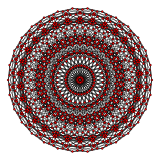
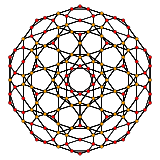
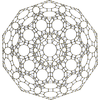
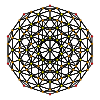
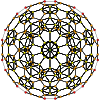
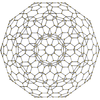
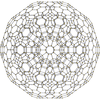
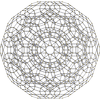
In 4-dimensional geometry, there are 15 uniform polytopes with H4 symmetry. Two of these, the 120-cell and 600-cell, are regular.
In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D4 symmetry, all are shared with higher symmetry constructions in the B4 or F4 symmetry families. there is also one half symmetry alternation, the snub 24-cell.