
In electromagnetism, there are two kinds of dipoles:
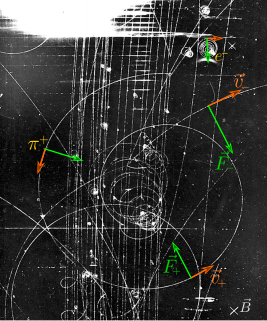
In physics the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force of

Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a magnetic field that varies with location will exert a force on a range of non-magnetic materials by affecting the motion of their outer atomic electrons. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

An electric field is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field for a system of charged particles. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental interactions of nature.

In electromagnetism, a magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the size of the source is reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric dipole, but the analogy is not perfect. In particular, a true magnetic monopole, the magnetic analogue of an electric charge, has never been observed in nature. However, magnetic monopole quasiparticles have been observed as emergent properties of certain condensed matter systems. Moreover, one form of magnetic dipole moment is associated with a fundamental quantum property—the spin of elementary particles.

Classical electromagnetism or classical electrodynamics is a branch of theoretical physics that studies the interactions between electric charges and currents using an extension of the classical Newtonian model. The theory provides a description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible. For small distances and low field strengths, such interactions are better described by quantum electrodynamics.

In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current, permanent magnets, elementary particles, various molecules, and many astronomical objects.

In electromagnetism, displacement current density is the quantity ∂D/∂t appearing in Maxwell's equations that is defined in terms of the rate of change of D, the electric displacement field. Displacement current density has the same units as electric current density, and it is a source of the magnetic field just as actual current is. However it is not an electric current of moving charges, but a time-varying electric field. In physical materials, there is also a contribution from the slight motion of charges bound in atoms, called dielectric polarization.

An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.

In classical electromagnetism, magnetic vector potential is the vector quantity defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
A classical field theory is a physical theory that predicts how one or more physical fields interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically meant to describe electromagnetism and gravitation, two of the fundamental forces of nature.

In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a gauge transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom.

In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Movement within this field is described by direction and is either Axial or Diametric. The origin of the magnetic moments responsible for magnetization can be either microscopic electric currents resulting from the motion of electrons in atoms, or the spin of the electrons or the nuclei. Net magnetization results from the response of a material to an external magnetic field. Paramagnetic materials have a weak induced magnetization in a magnetic field, which disappears when the magnetic field is removed. Ferromagnetic and ferrimagnetic materials have strong magnetization in a magnetic field, and can be magnetized to have magnetization in the absence of an external field, becoming a permanent magnet. Magnetization is not necessarily uniform within a material, but may vary between different points. Magnetization also describes how a material responds to an applied magnetic field as well as the way the material changes the magnetic field, and can be used to calculate the forces that result from those interactions. It can be compared to electric polarization, which is the measure of the corresponding response of a material to an electric field in electrostatics. Physicists and engineers usually define magnetization as the quantity of magnetic moment per unit volume. It is represented by a pseudovector M.

In electromagnetism and applications, an inhomogeneous electromagnetic wave equation, or nonhomogeneous electromagnetic wave equation, is one of a set of wave equations describing the propagation of electromagnetic waves generated by nonzero source charges and currents. The source terms in the wave equations make the partial differential equations inhomogeneous, if the source terms are zero the equations reduce to the homogeneous electromagnetic wave equations. The equations follow from Maxwell's equations.

There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.

The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb-meter (C⋅m). The debye (D) is another unit of measurement used in atomic physics and chemistry.
Multipole radiation is a theoretical framework for the description of electromagnetic or gravitational radiation from time-dependent distributions of distant sources. These tools are applied to physical phenomena which occur at a variety of length scales - from gravitational waves due to galaxy collisions to gamma radiation resulting from nuclear decay. Multipole radiation is analyzed using similar multipole expansion techniques that describe fields from static sources, however there are important differences in the details of the analysis because multipole radiation fields behave quite differently from static fields. This article is primarily concerned with electromagnetic multipole radiation, although the treatment of gravitational waves is similar.

Magnetic current is, nominally, a current composed of fictitious moving magnetic monopoles. It has the dimensions of volts. The usual symbol for magnetic current is which is analogous to for electric current. Magnetic currents produce an electric field analogously to the production of a magnetic field by electric currents. Magnetic current density, which has the units of V/m2, is usually represented by the symbols and . The superscripts indicate total and impressed magnetic current density. The impressed currents are the energy sources. In many useful cases, a distribution of electric charge can be mathematically replaced by an equivalent distribution of magnetic current. This artifice can be used to simplify some electromagnetic field problems. It is possible to use both electric current densities and magnetic current densities in the same analysis.













































































