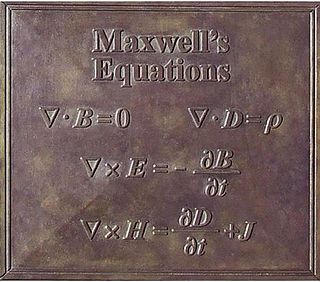Electromechanics
After Maxwell proposed the differential equation model of the electromagnetic field in 1873, the mechanism of action of fields came into question, for instance in the Kelvin's master class held at Johns Hopkins University in 1884 and commemorated a century later. [1]
The requirement that the equations remain consistent when viewed from various moving observers led to special relativity, a geometric theory of 4-space where intermediation is by light and radiation. [2] The spacetime geometry provided a context for technical description of electric technology, especially generators, motors, and lighting at first. The Coulomb force was generalized to the Lorentz force. For example, with this model transmission lines and power grids were developed and radio frequency communication explored.
An effort to mount a full-fledged electromechanics on a relativistic basis is seen in the work of Leigh Page, from the project outline in 1912 [3] to his textbook Electrodynamics (1940) [4] The interplay (according to the differential equations) of electric and magnetic field as viewed over moving observers is examined. What is charge density in electrostatics becomes proper charge density [5] [6] [7] and generates a magnetic field for a moving observer.
A revival of interest in this method for education and training of electrical and electronics engineers broke out in the 1960s after Richard Feynman's textbook. [8] Rosser's book Classical Electromagnetism via Relativity was popular, [9] as was Anthony French's treatment in his textbook [10] which illustrated diagrammatically the proper charge density. One author proclaimed, "Maxwell — Out of Newton, Coulomb, and Einstein". [11]
The use of retarded potentials to describe electromagnetic fields from source-charges is an expression of relativistic electromagnetism.

In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, which are distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles. Electric forces cause an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs between charged particles in relative motion. These two forces are described in terms of electromagnetic fields. Macroscopic charged objects are described in terms of Coulomb's law for electricity and Ampère's force law for magnetism; the Lorentz force describes microscopic charged particles.

An electromagnetic field is a physical field, mathematical functions of position and time, representing the influences on and due to electric charges. The field at any point in space and time can be regarded as a combination of an electric field and a magnetic field. Because of the interrelationship between the fields, a disturbance in the electric field can create a disturbance in the magnetic field which in turn affects the electric field, leading to an oscillation that propagates through space, known as an electromagnetic wave.
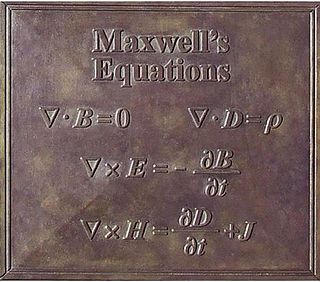
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.

In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 paper, On the Electrodynamics of Moving Bodies, the theory is presented as being based on just two postulates:
- The laws of physics are invariant (identical) in all inertial frames of reference. This is known as the principle of relativity.
- The speed of light in vacuum is the same for all observers, regardless of the motion of light source or observer. This is known as the principle of light constancy, or the principle of light speed invariance.

A magnetic field is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

An electric field is the physical field that surrounds electrically charged particles. Charged particles exert attractive forces on each other when their charges are opposite, and repulse each other when their charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. The electric field of a single charge describes their capacity to exert such forces on another charged object. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Thus, we may informally say that the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker further away. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, Electromagnetism is one of the four fundamental interactions of nature.

Classical electromagnetism or classical electrodynamics is a branch of theoretical physics that studies the interactions between electric charges and currents using an extension of the classical Newtonian model. It is, therefore, a classical field theory. The theory provides a description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible. For small distances and low field strengths, such interactions are better described by quantum electrodynamics which is a quantum field theory.
Action at a distance is the concept in physics that an object's motion can be affected by another object without the two being in physical contact; that is, it is the concept of the non-local interaction of objects that are separated in space. Coulomb's law and Newton's law of universal gravitation are based on action at a distance.
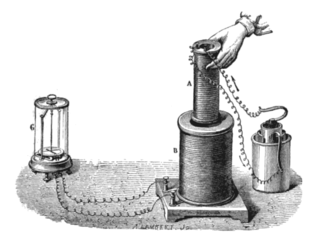
Faraday's law of induction is a law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (emf). This phenomenon, known as electromagnetic induction, is the fundamental operating principle of transformers, inductors, and many types of electric motors, generators and solenoids.
Albert Einstein derived the theory of special relativity in 1905, from principle now called the postulates of special relativity. Einstein's formulation is said to only require two postulates, though his derivation implies a few more assumptions.
The history of special relativity consists of many theoretical results and empirical findings obtained by Albert A. Michelson, Hendrik Lorentz, Henri Poincaré and others. It culminated in the theory of special relativity proposed by Albert Einstein and subsequent work of Max Planck, Hermann Minkowski and others.

In electromagnetism, Jefimenko's equations give the electric field and magnetic field due to a distribution of electric charges and electric current in space, that takes into account the propagation delay of the fields due to the finite speed of light and relativistic effects. Therefore, they can be used for moving charges and currents. They are the particular solutions to Maxwell's equations for any arbitrary distribution of charges and currents.
Heaviside–Lorentz units constitute a system of units and quantities that extends the CGS with a particular set of equations that defines electromagnetic quantities, named for Oliver Heaviside and Hendrik Antoon Lorentz. They share with the CGS-Gaussian system that the electric constant ε0 and magnetic constant µ0 do not appear in the defining equations for electromagnetism, having been incorporated implicitly into the electromagnetic quantities. Heaviside–Lorentz units may be thought of as normalizing ε0 = 1 and µ0 = 1, while at the same time revising Maxwell's equations to use the speed of light c instead.

The moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in the frame of reference of the magnet and in the frame of reference of the conductor. The observable quantity in the experiment, the current, is the same in either case, in accordance with the basic principle of relativity, which states: "Only relative motion is observable; there is no absolute standard of rest". However, according to Maxwell's equations, the charges in the conductor experience a magnetic force in the frame of the magnet and an electric force in the frame of the conductor. The same phenomenon would seem to have two different descriptions depending on the frame of reference of the observer.

The theory of special relativity plays an important role in the modern theory of classical electromagnetism. It gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of reference to another. It sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electric or magnetic laws. It motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.

In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. An example of a scalar field is a weather map, with the surface temperature described by assigning a number to each point on the map. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field.

The Feynman Lectures on Physics is a physics textbook based on a great number of lectures by Richard Feynman, a Nobel laureate who has sometimes been called "The Great Explainer". The lectures were presented before undergraduate students at the California Institute of Technology (Caltech), during 1961–1964. The book's co-authors are Feynman, Robert B. Leighton, and Matthew Sands.

By the first half of the 19th century, the understanding of electromagnetics had improved through many experiments and theoretical work. In the 1780s, Charles-Augustin de Coulomb established his law of electrostatics. In 1825, André-Marie Ampère published his force law. In 1831, Michael Faraday discovered electromagnetic induction through his experiments, and proposed lines of forces to describe it. In 1834, Emil Lenz solved the problem of the direction of the induction, and Franz Ernst Neumann wrote down the equation to calculate the induced force by change of magnetic flux. However, these experimental results and rules were not well organized and sometimes confusing to scientists. A comprehensive summary of the electrodynamic principles was needed.
Galilean electromagnetism is a formal electromagnetic field theory that is consistent with Galilean invariance. Galilean electromagnetism is useful for describing the electric and magnetic fields in the vicinity of charged bodies moving at non-relativistic speeds relative to the frame of reference. The resulting mathematical equations are simpler than the fully relativistic forms because certain coupling terms are neglected.
Electromagnetism is one of the fundamental forces of nature. Early on, electricity and magnetism were studied separately and regarded as separate phenomena. Hans Christian Ørsted discovered that the two were related – electric currents give rise to magnetism. Michael Faraday discovered the converse, that magnetism could induce electric currents, and James Clerk Maxwell put the whole thing together in a unified theory of electromagnetism. Maxwell's equations further indicated that electromagnetic waves existed, and the experiments of Heinrich Hertz confirmed this, making radio possible. Maxwell also postulated, correctly, that light was a form of electromagnetic wave, thus making all of optics a branch of electromagnetism. Radio waves differ from light only in that the wavelength of the former is much longer than the latter. Albert Einstein showed that the magnetic field arises through the relativistic motion of the electric field and thus magnetism is merely a side effect of electricity. The modern theoretical treatment of electromagnetism is as a quantum field in quantum electrodynamics.