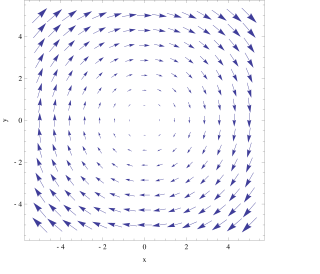
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.

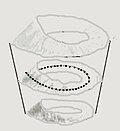
In mathematics, the Klein bottle is an example of a non-orientable surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with a boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.
In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form a + bε, where a and b are real numbers, and ε is a symbol taken to satisfy with .

In mathematics, genus has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1.

In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space . A vector field on a plane can be visualized as a collection of arrows with given magnitudes and directions, each attached to a point on the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout three dimensional space, such as the wind, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.

Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems published by mathematician Emmy Noether in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries of physical space.

In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "anticlockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space.
In the mathematical field of Riemannian geometry, the scalar curvature is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry of the metric near that point. It is defined by a complicated explicit formula in terms of partial derivatives of the metric components, although it is also characterized by the volume of infinitesimally small geodesic balls. In the context of the differential geometry of surfaces, the scalar curvature is twice the Gaussian curvature, and completely characterizes the curvature of a surface. In higher dimensions, however, the scalar curvature only represents one particular part of the Riemann curvature tensor.
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form of one complex variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.

In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set in a Euclidean space , or more generally in a metric space . It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand.
A Seifert fiber space is a 3-manifold together with a decomposition as a disjoint union of circles. In other words, it is a -bundle over a 2-dimensional orbifold. Many 3-manifolds are Seifert fiber spaces, and they account for all compact oriented manifolds in 6 of the 8 Thurston geometries of the geometrization conjecture.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

A Gaussian surface is a closed surface in three-dimensional space through which the flux of a vector field is calculated; usually the gravitational field, electric field, or magnetic field. It is an arbitrary closed surface S = ∂V used in conjunction with Gauss's law for the corresponding field by performing a surface integral, in order to calculate the total amount of the source quantity enclosed; e.g., amount of gravitational mass as the source of the gravitational field or amount of electric charge as the source of the electrostatic field, or vice versa: calculate the fields for the source distribution.
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one finite-dimensional manifold from another in a 'controlled' way, introduced by John Milnor. Milnor called this technique surgery, while Andrew Wallace called it spherical modification. The "surgery" on a differentiable manifold M of dimension , could be described as removing an imbedded sphere of dimension p from M. Originally developed for differentiable manifolds, surgery techniques also apply to piecewise linear (PL-) and topological manifolds.
In the field of mathematics known as differential geometry, a generalized complex structure is a property of a differential manifold that includes as special cases a complex structure and a symplectic structure. Generalized complex structures were introduced by Nigel Hitchin in 2002 and further developed by his students Marco Gualtieri and Gil Cavalcanti.
In mathematics, Liouville's theorem, proved by Joseph Liouville in 1850, is a rigidity theorem about conformal mappings in Euclidean space. It states that every smooth conformal mapping on a domain of Rn, where n > 2, can be expressed as a composition of translations, similarities, orthogonal transformations and inversions: they are Möbius transformations. This theorem severely limits the variety of possible conformal mappings in R3 and higher-dimensional spaces. By contrast, conformal mappings in R2 can be much more complicated – for example, all simply connected planar domains are conformally equivalent, by the Riemann mapping theorem.
In mathematics, specifically the theory of quadratic forms, an ε-quadratic form is a generalization of quadratic forms to skew-symmetric settings and to *-rings; ε = ±1, accordingly for symmetric or skew-symmetric. They are also called -quadratic forms, particularly in the context of surgery theory.