Orbital station-keeping

Last updated

In astrodynamics, orbital station-keeping is keeping a spacecraft at a fixed distance from another spacecraft or celestial body. It requires a series of orbital maneuvers made with thruster burns to keep the active craft in the same orbit as its target. For many low Earth orbit satellites, the effects of non-Keplerian forces, i.e. the deviations of the gravitational force of the Earth from that of a homogeneous sphere, gravitational forces from Sun/Moon, solar radiation pressure and air drag, must be counteracted. For spacecraft in a halo orbit around a Lagrange point, station-keeping is even more fundamental, as such an orbit is unstable; without an active control with thruster burns, the smallest deviation in position or velocity would result in the spacecraft leaving orbit completely. [1]

Contents

Perturbations

The deviation of Earth's gravity field from that of a homogeneous sphere and gravitational forces from the Sun and Moon will in general perturb the orbital plane. For a Sun-synchronous orbit, the precession of the orbital plane caused by the oblateness of the Earth is a desirable feature that is part of mission design but the inclination change caused by the gravitational forces of the Sun and Moon is undesirable. For geostationary spacecraft, the inclination change caused by the gravitational forces of the Sun and Moon must be counteracted by a rather large expense of fuel, as the inclination should be kept sufficiently small for the spacecraft to be tracked by non-steerable antennae.

For spacecraft in a low orbit, the effects of atmospheric drag must often be compensated for, often to avoid re-entry; for missions requiring the orbit to be accurately synchronized with the Earth’s rotation, this is necessary to prevent a shortening of the orbital period.

Solar radiation pressure will in general perturb the eccentricity (i.e. the eccentricity vector); see Orbital perturbation analysis (spacecraft). For some missions, this must be actively counter-acted with maneuvers. For geostationary spacecraft, the eccentricity must be kept sufficiently small for a spacecraft to be tracked with a non-steerable antenna. Also for Earth observation spacecraft for which a very repetitive orbit with a fixed ground track is desirable, the eccentricity vector should be kept as fixed as possible. A large part of this compensation can be done by using a frozen orbit design, but often thrusters are needed for fine control maneuvers.

Low Earth orbit

For spacecraft in a very low orbit, the atmospheric drag is sufficiently strong to cause a re-entry before the intended end of mission if orbit raising maneuvers are not executed from time to time.

An example of this is the International Space Station (ISS), which has an operational altitude above Earth's surface of between 400 and 430 km (250-270 mi). Due to atmospheric drag the space station is constantly losing orbital energy. In order to compensate for this loss, which would eventually lead to a re-entry of the station, it has to be reboosted to a higher orbit from time to time. The chosen orbital altitude is a trade-off between the average thrust needed to counter-act the air drag and the impulse needed to send payloads and people to the station.

GOCE which orbited at 255 km (later reduced to 235 km) used ion thrusters to provide up to 20 mN of thrust to compensate for the drag on its frontal area of about 1 m2. [2]

Earth observation spacecraft

For Earth observation spacecraft typically operated in an altitude above the Earth surface of about 700 – 800 km the air-drag is very faint and a re-entry due to air-drag is not a concern. But if the orbital period should be synchronous with the Earth's rotation to maintain a fixed ground track, the faint air-drag at this high altitude must also be counter-acted by orbit raising maneuvers in the form of thruster burns tangential to the orbit. These maneuvers will be very small, typically in the order of a few mm/s of delta-v. If a frozen orbit design is used these very small orbit raising maneuvers are sufficient to also control the eccentricity vector.

To maintain a fixed ground track it is also necessary to make out-of-plane maneuvers to compensate for the inclination change caused by Sun/Moon gravitation. These are executed as thruster burns orthogonal to the orbital plane. For Sun-synchronous spacecraft having a constant geometry relative to the Sun, the inclination change due to the solar gravitation is particularly large; a delta-v in the order of 1–2 m/s per year can be needed to keep the inclination constant. [ citation needed ]

Geostationary orbit

Inclined orbital planes Orbital Planes.svg
Inclined orbital planes

For geostationary spacecraft, thruster burns orthogonal to the orbital plane must be executed to compensate for the effect of the lunar/solar gravitation that perturbs the orbit pole with typically 0.85 degrees per year. [3] The delta-v needed to compensate for this perturbation keeping the inclination to the equatorial plane amounts to in the order 45 m/s per year. This part of the GEO station-keeping is called North-South control. [4]

The East-West control is the control of the orbital period and the eccentricity vector performed by making thruster burns tangential to the orbit. These burns are then designed to keep the orbital period perfectly synchronous with the Earth rotation and to keep the eccentricity sufficiently small. Perturbation of the orbital period results from the imperfect rotational symmetry of the Earth relative the North/South axis, sometimes called the ellipticity of the Earth equator. The eccentricity (i.e. the eccentricity vector) is perturbed by the solar radiation pressure. The fuel needed for this East-West control is much less than what is needed for the North-South control.

To extend the life-time of geostationary spacecraft with little fuel left one sometimes discontinues the North-South control only continuing with the East-West control. As seen from an observer on the rotating Earth the spacecraft will then move North-South with a period of 24 hours. When this North-South movement gets too large a steerable antenna is needed to track the spacecraft. An example of this[ when? ] is Artemis.[ citation needed ]

To save weight, it is crucial for GEO satellites to have the most fuel-efficient propulsion system. Almost all modern satellites are therefore employing a high specific impulse system like plasma or ion thrusters.

Lagrange points

Orbits of spacecraft are also possible around Lagrange points—also referred to as libration points—five equilibrium points that exist in relation to two larger solar system bodies. For example, there are five of these points in the Sun-Earth system, five in the Earth-Moon system, and so on. Spacecraft may orbit around these points with a minimum of propellant required for station-keeping purposes. Two orbits that have been used for such purposes include halo and Lissajous orbits. [5]

One important Lagrange point is Earth-Sun L1, and three heliophysics missions have been orbiting L1 since approximately 2000. Station-keeping propellant use can be quite low, facilitating missions that can potentially last decades should other spacecraft systems remain operational. The three spacecraft—Advanced Composition Explorer (ACE), Solar Heliospheric Observatory (SOHO), and the Global Geoscience WIND satellite—each have annual station-keeping propellant requirements of approximately 1 m/s or less. [5] Earth-Sun L2—approximately 1.5 million kilometers from Earth in the anti-sun direction—is another important Lagrange point, and the ESA Herschel space observatory operated there in a Lissajous orbit during 2009–2013, at which time it ran out of coolant for the space telescope. Small station-keeping orbital maneuvers were executed approximately monthly to maintain the spacecraft in the station-keeping orbit. [1]

The James Webb Space Telescope will use propellant to maintain its halo orbit around the Earth-Sun L2, which provides an upper limit to its designed lifetime: it is being designed to carry enough for ten years. [6] However, the precision of trajectory following launch by an Ariane 5 is credited with potentially doubling the lifetime of the telescope by leaving more hydrazine propellant on-board than expected. [7] [8]

The CAPSTONE orbiter and the planned Lunar Gateway is stationed along a 9:2 synodically resonant Near Rectilinear Halo Orbit (NRHO) around the Earth-Moon L2 Lagrange point. [9] [10] [11]

See also

Related Research Articles

<span class="mw-page-title-main">Lagrange point</span> Equilibrium points near two orbiting bodies

In celestial mechanics, the Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem.

<span class="mw-page-title-main">Spacecraft propulsion</span> Method used to accelerate spacecraft

Spacecraft propulsion is any method used to accelerate spacecraft and artificial satellites. In-space propulsion exclusively deals with propulsion systems used in the vacuum of space and should not be confused with space launch or atmospheric entry.

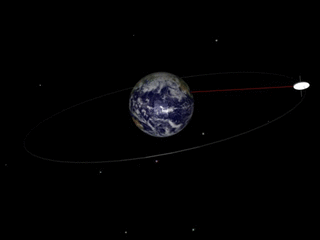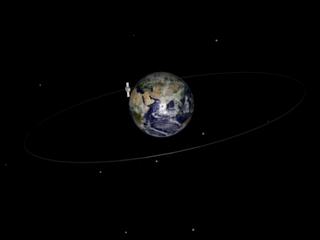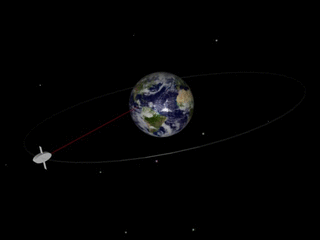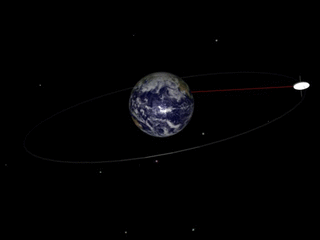
<span class="mw-page-title-main">Geosynchronous orbit</span> Orbit keeping the satellite at a fixed longitude above the equator

A geosynchronous orbit is an Earth-centered orbit with an orbital period that matches Earth's rotation on its axis, 23 hours, 56 minutes, and 4 seconds. The synchronization of rotation and orbital period means that, for an observer on Earth's surface, an object in geosynchronous orbit returns to exactly the same position in the sky after a period of one sidereal day. Over the course of a day, the object's position in the sky may remain still or trace out a path, typically in a figure-8 form, whose precise characteristics depend on the orbit's inclination and eccentricity. A circular geosynchronous orbit has a constant altitude of 35,786 km (22,236 mi).

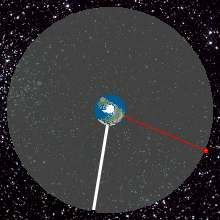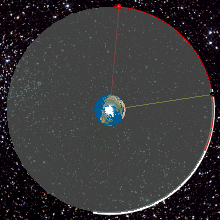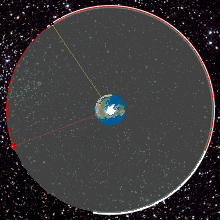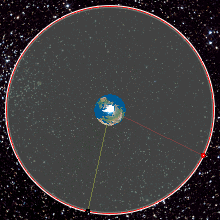
<span class="mw-page-title-main">Geostationary orbit</span> Circular orbit above Earths Equator and following the direction of Earths rotation

A geostationary orbit, also referred to as a geosynchronous equatorial orbit (GEO), is a circular geosynchronous orbit 35,786 km (22,236 mi) in altitude above Earth's equator, 42,164 km (26,199 mi) in radius from Earth's center, and following the direction of Earth's rotation.

<span class="mw-page-title-main">Geostationary transfer orbit</span> Transfer orbit used to reach geosynchronous or geostationary orbit

In space mission design, a geostationary transfer orbit (GTO) or geosynchronous transfer orbit is a highly elliptical type of geocentric orbit, usually with a perigee as low as low Earth orbit (LEO) and an apogee as high as geostationary orbit (GEO). Satellites that are destined for geosynchronous orbit (GSO) or GEO are often put into a GTO as an intermediate step for reaching their final orbit. Manufacturers of launch vehicles often advertise the amount of payload the vehicle can put into GTO.

<span class="mw-page-title-main">Interplanetary Transport Network</span> Low-energy trajectories in the Solar System

The Interplanetary Transport Network (ITN) is a collection of gravitationally determined pathways through the Solar System that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space can be redirected using little or no energy. These points have the peculiar property of allowing objects to orbit around them, despite lacking an object to orbit, as these points exist where gravitational forces between two celestial bodies are equal. While it would use little energy, transport along the network would take a long time.

Delta-v, symbolized as and pronounced ,as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launching from or landing on a planet or moon, or an in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of said spacecraft.

<span class="mw-page-title-main">Orbital spaceflight</span> Spaceflight where spacecraft orbits an astronomical body

An orbital spaceflight is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altitude at perigee around 80 kilometers (50 mi); this is the boundary of space as defined by NASA, the US Air Force and the FAA. To remain in orbit at this altitude requires an orbital speed of ~7.8 km/s. Orbital speed is slower for higher orbits, but attaining them requires greater delta-v. The Fédération Aéronautique Internationale has established the Kármán line at an altitude of 100 km (62 mi) as a working definition for the boundary between aeronautics and astronautics. This is used because at an altitude of about 100 km (62 mi), as Theodore von Kármán calculated, a vehicle would have to travel faster than orbital velocity to derive sufficient aerodynamic lift from the atmosphere to support itself.

Delta-<i>v</i> budget Estimate of total change in velocity of a space mission

In astrodynamics and aerospace, a delta-v budget is an estimate of the total change in velocity (delta-v) required for a space mission. It is calculated as the sum of the delta-v required to perform each propulsive maneuver needed during the mission. As input to the Tsiolkovsky rocket equation, it determines how much propellant is required for a vehicle of given empty mass and propulsion system.

<span class="mw-page-title-main">Graveyard orbit</span> Spacecraft end-of-life orbit

A graveyard orbit, also called a junk orbit or disposal orbit, is an orbit that lies away from common operational orbits. One significant graveyard orbit is a supersynchronous orbit well beyond geosynchronous orbit. Some satellites are moved into such orbits at the end of their operational life to reduce the probability of colliding with operational spacecraft and generating space debris.

<span class="mw-page-title-main">Spacecraft flight dynamics</span> Application of mechanical dynamics to model the flight of space vehicles

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

<span class="mw-page-title-main">International Cometary Explorer</span> NASA satellite of the Explorer program

The International Cometary Explorer (ICE) spacecraft, designed and launched as the International Sun-Earth Explorer-3 (ISEE-3) satellite, was launched on 12 August 1978 into a heliocentric orbit. It was one of three spacecraft, along with the mother/daughter pair of ISEE-1 and ISEE-2, built for the International Sun-Earth Explorer (ISEE) program, a joint effort by NASA and ESRO/ESA to study the interaction between the Earth's magnetic field and the solar wind.

In spaceflight an orbit insertion is an orbital maneuver which adjusts a spacecraft’s trajectory, allowing entry into an orbit around a planet, moon, or other celestial body. An orbit insertion maneuver involves either deceleration from a speed in excess of the respective body's escape velocity, or acceleration to it from a lower speed.

This is an alphabetical list of articles pertaining specifically to aerospace engineering. For a broad overview of engineering, see List of engineering topics. For biographies, see List of engineers.

<span class="mw-page-title-main">Halo orbit</span> Periodic, three-dimensional orbit

A halo orbit is a periodic, three-dimensional orbit associated with one of the L1, L2 or L3 Lagrange points in the three-body problem of orbital mechanics. Although a Lagrange point is just a point in empty space, its peculiar characteristic is that it can be orbited by a Lissajous orbit or by a halo orbit. These can be thought of as resulting from an interaction between the gravitational pull of the two planetary bodies and the Coriolis and centrifugal force on a spacecraft. Halo orbits exist in any three-body system, e.g., a Sun–Earth–orbiting satellite system or an Earth–Moon–orbiting satellite system. Continuous "families" of both northern and southern halo orbits exist at each Lagrange point. Because halo orbits tend to be unstable, station-keeping using thrusters may be required to keep a satellite on the orbit.

<span class="mw-page-title-main">Aditya-L1</span> Indias first solar observation mission

Aditya-L1 is a coronagraphy spacecraft for studying the solar atmosphere, designed and developed by the Indian Space Research Organisation (ISRO) and various other Indian Space Research Institutes. It is orbiting at about 1.5 million km from Earth in a halo orbit around the Lagrange point 1 (L1) between the Earth and the Sun, where it will study the solar atmosphere, solar magnetic storms, and their impact on the environment around the Earth.

In orbital mechanics, a frozen orbit is an orbit for an artificial satellite in which perturbations have been minimized by careful selection of the orbital parameters. Perturbations can result from natural drifting due to the central body's shape, or other factors. Typically, the altitude of a satellite in a frozen orbit remains constant at the same point in each revolution over a long period of time. Variations in the inclination, position of the apsis of the orbit, and eccentricity have been minimized by choosing initial values so that their perturbations cancel out. This results in a long-term stable orbit that minimizes the use of station-keeping propellant.

<span class="mw-page-title-main">Near-rectilinear halo orbit</span> Periodic, three-dimensional circuit associated with a Lagrange point in the three-body problem

In orbital mechanics a near-rectilinear halo orbit (NRHO) is a halo orbit that passes close to the smaller of two bodies and has nearly stable behavior. The CAPSTONE mission, launched in 2022, is the first spacecraft to use such orbit in cislunar space, and this Moon-centric orbit is planned as a staging area for future lunar missions. In contrast with low lunar orbit which NASA characterizes as being deep in the lunar gravity well, NRHO is described as being "balanced on the edge" of the gravity well.

References

  1. 1 2 "ESA Science & Technology: Orbit/Navigation". European Space Agency. 14 June 2009. Retrieved 14 February 2015.
  2. ↑ "GOCE satellite".
  3. ↑ Anderson, Paul; et al. (2015). Operational Considerations of GEO Debris Synchronization Dynamics (PDF). 66th International Astronautical Congress. Jerusalem, Israel. IAC-15,A6,7,3,x27478.
  4. ↑ Soop, E. M. (1994). Handbook of Geostationary Orbits. Springer. ISBN   978-0-7923-3054-7.
  5. 1 2 Roberts, Craig E. (1 January 2011). "Long Term Missions at the Sun-Earth Libration Point L1: ACE, SOHO, and WIND". NASA Technical Reports. NASA. hdl:2060/20110008638. 20110008638. Three heliophysics missions – the Advanced Composition Explorer (ACE), Solar Heliospheric Observatory (SOHO), and the Global Geoscience WIND – have been orbiting the Sun-Earth interior libration point L1 continuously since 1997, 1996, and 2004 ... the typical interval between burns for this trio is about three months, and the typical delta-V is much smaller than 0.5 m/sec. Typical annual stationkeeping costs have been around 1.0 m/sec for ACE and WIND, and much less than that for SOHO. All three spacecraft have ample fuel remaining; barring contingencies all three could, in principle, be maintained at L1 for decades to come.
  6. ↑ "FAQ Full General Public Webb Telescope/NASA". jwst.nasa.gov.
  7. ↑ Amos, Jonathan (January 9, 2022). "James Webb telescope completes epic deployment sequence". www.bbc.com. BBC News . Retrieved January 10, 2022.
  8. ↑ Berger, Eric (10 January 2022). "All hail the Ariane 5 rocket, which doubled the Webb telescope's lifetime". www.arstechnica.com. Ars Technica . Retrieved 11 January 2022.
  9. ↑ Muralidharan, Vivek; Howell, Kathleen (2020). Stationkeeping in Earth-Moon Near Rectilinear Halo Orbits (PDF). AAS/AIAA Astrodynamics Specialist Conference. South Lake Tahoe, California, USA. AAS 20-642.
  10. ↑ Newman, Clark P.; et al. (2018). Stationkeeping, orbit determination, and attitude control for spacecraft in near rectilinear halo orbits. AAS/AIAA Astrodynamics Specialist Conference. Snowbird, Utah, USA. AAS 18-388.
  11. ↑ Muralidharan, Vivek; Howell, Kathleen (2022). "Leveraging stretching directions for stationkeeping in Earth-Moon halo orbits". Advances in Space Research . 69 (1): 620–646. Bibcode:2022AdSpR..69..620M. doi:10.1016/j.asr.2021.10.028. S2CID   239490016.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.