
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number ,a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world.

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.
In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example with three indeterminates is x3 + 2xyz2 − yz + 1.

In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure that resembles a group in the sense that "division" is always possible. Quasigroups differ from groups mainly in that the associative and identity element properties are optional. In fact, a nonempty associative quasigroup is a group.

The imaginary unit or unit imaginary number is a mathematical constant that is a solution to the quadratic equation x2 + 1 = 0. Although there is no real number with this property, i can be used to extend the real numbers to what are called complex numbers, using addition and multiplication. A simple example of the use of i in a complex number is 2 + 3i.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
In arithmetic and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common divisor (gcd) of integers a and b, also the coefficients of Bézout's identity, which are integers x and y such that

In mathematics, exponentiation is an operation involving two numbers: the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; often said as "b to the power n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases: In particular, .
In mathematics, the Cayley–Dickson construction, sometimes also known as the Cayley–Dickson process or the Cayley–Dickson procedure produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one. It is named after Arthur Cayley and Leonard Eugene Dickson. The algebras produced by this process are known as Cayley–Dickson algebras, for example complex numbers, quaternions, and octonions. These examples are useful composition algebras frequently applied in mathematical physics.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.
In mathematics, the additive inverse of an element x, denoted -x, is the element that when added to x, yields the additive identity, 0 (zero). In the most familiar cases, this is the number 0, but it can also refer to a more generalized zero element.

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function f(x) that maps x to 1/x, is one of the simplest examples of a function which is its own inverse (an involution).
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.
In mathematics, an expression or equation is in closed form if it is formed with constants, variables and a finite set of basic functions connected by arithmetic operations and function composition. Commonly, the allowed functions are nth root, exponential function, logarithm, and trigonometric functions. However, the set of basic functions depends on the context.
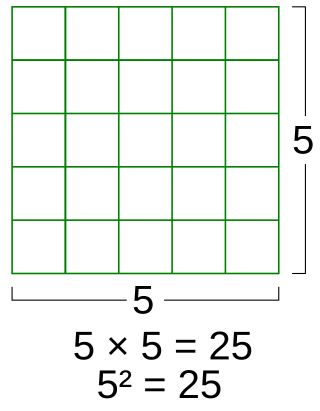
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
In mathematics, an algebraic function is a function that can be defined as the root of an irreducible polynomial equation. Algebraic functions are often algebraic expressions using a finite number of terms, involving only the algebraic operations addition, subtraction, multiplication, division, and raising to a fractional power. Examples of such functions are:

In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion.

In mathematics, an infinite sequence of numbers is called constant-recursive if it satisfies an equation of the form











